В природном ландшафте есть холмы и долины. Чтобы забраться на холм, необходимо затратить энергию, но поезд может и набрать энергию, скатившись с холма в долину. Здесь в действие вступают два типа энергии. Высота над уровнем моря определяет потенциальную энергию поезда, посредством которой проявляется сила тяготения. Еще существует кинетическая энергия, которая соответствует скорости. Когда поезд катится с горки и ускоряется, он тем самым обменивает потенциальную энергию на кинетическую. Когда он взбирается на холм и замедляется, происходит обратный обмен. Полная энергия поезда постоянна, так что движение происходит по горизонтали энергетического ландшафта. Однако у поездов имеется третий источник энергии: топливо. Сжигая дизельное топливо или используя электричество, поезд может взобраться на горку или ускориться, уходя при этом от естественной, «свободной» траектории. В любой момент времени полная энергия должна оставаться неизменной, но обо всем остальном можно договориться.
Примерно так же обстоит дело с космическими аппаратами. Гравитационные поля Солнца, планет и других тел обеспечивают потенциальную энергию. Скорость аппарата соответствует его кинетической энергии. А его движитель — это дополнительный источник энергии, который можно произвольно включать и выключать. Энергия здесь играет ту же роль, что высота в земном ландшафте, а траектория космического аппарата представляет собой своего рода горизонталь, вдоль которой его полная энергия остается постоянной. Принципиально важно, что вам необязательно все время находиться на одной горизонтали: вы можете сжечь некоторое количество топлива, чтобы перейти на другую горизонталь, сдвинувшись при этом «вверх по склону» или «вниз по склону».
Фокус в том, чтобы сделать это в нужном месте. Инженеры-железнодорожники викторианской эпохи хорошо понимали, что в земном ландшафте есть особые черты — это может быть вершина холма, дно долины, седловидная геометрия горного перевала. Эти черты принципиально важны: они образуют своего рода скелет, основу общей геометрии горизонталей. К примеру, вблизи любой вершины горизонтали представляют собой замкнутые кривые. На вершине потенциальная энергия принимает локально максимальное значение, а на дне долины — локально минимальное. Перевалы сочетают в себе черты того и другого — это максимум для одних направлений и минимум для других — и позволяют преодолевать горы с минимальными усилиями.
Аналогично в энергетическом ландшафте Солнечной системы тоже есть особые детали. Самые очевидные из них — Солнце, планеты и луны, располагающиеся на дне гравитационных колодцев. Не менее важны, хотя и менее заметны на энергетическом ландшафте, холмы, низины и перевалы. Эти черты организуют общую геометрию ландшафта, и именно эта геометрия порождает трубки, о которых мы говорили. Самыми известными деталями энергетического ландшафта, помимо гравитационных колодцев, являются точки Лагранжа.
Около 1985 года Эдвард Белбруно впервые использовал хаотическую динамику при планировании межпланетного перелета, предложив то, что позже получило название теории нечетких границ. Он понял, что трубки в сочетании с хаосом определяют новые энергетически эффективные маршруты между мирами. Маршруты эти строятся из кусочков естественных орбит в системах трех тел, где имеются новые детали, такие, к примеру, как точки Лагранжа. Один из способов найти их состоит в том, чтобы начать с середины, а затем двигаться наружу. Представьте себе космический аппарат в точке L1 системы Земля — Луна, между двумя этими небесными телами. Если этому телу дать совсем небольшой толчок, он покатится «вниз», теряя потенциальную энергию и набирая кинетическую. В некоторых случаях толчок может направить аппарат в сторону Земли, где он со временем выйдет на орбиту вокруг нашей родной планеты. В других случаях толчок направит аппарат в сторону Луны, на лунную орбиту захвата. Взяв маршрут от L1 до Земли в обратном направлении и прицепив к нему подходящий маршрут от L1 до Луны, мы получим весьма эффективную траекторию от Земли к Луне с переходом в точке L1.
Оказывается, точка L1 — отличное место для небольших изменений курса. Естественная динамика космического аппарата возле L1 хаотична, так что очень небольшие изменения положения или скорости очень серьезно меняют траекторию. Воспользовавшись хаосом, мы можем перенаправить наш космический аппарат в другое место назначения эффективным по топливу, хотя, возможно, и медленным образом.
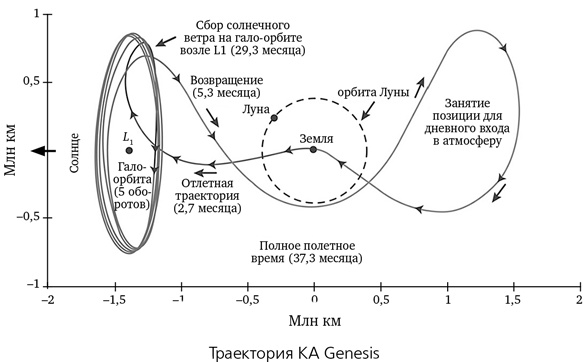
Фокус с трубкой был впервые использован, чтобы перенаправить почти выработавший ресурс аппарат ISEE-3 (расшифровывается как Международный исследователь солнечно-земных связей) на встречу в 1985 году с кометой Джакобини — Циннера. В 1990 году Белбруно связался с Японским космическим агентством по поводу одного из их аппаратов — лунного зонда Hiten, завершившего свою основную программу, но еще имевшего в баках немного топлива. Он представил агентству траекторию, которая должна была временно стабилизировать аппарат на окололунной орбите, а затем перенаправить его в точки L4 и L5 на поиски захваченных пылевых частиц. Тот же фокус был использован вновь, чтобы аппарат проекта Genesis смог доставить на Землю образцы частиц солнечного ветра.
Математики и инженеры, которым захотелось повторить этот трюк и найти другие возможности того же рода, попытались разобраться, на чем основан механизм его действия. Они сосредоточили внимание на особых объектах энергетического ландшафта, аналогичных горным перевалам. В этих местах на маршрутах возникают «бутылочные горлышки», и аппараты, которым необходимо попасть на нужную траекторию, должны преодолевать их очень аккуратно. Существуют отдельные «входящие» и «выходящие» траектории, аналогичные естественным проходам в горах. Чтобы точно пройти по этим входящим и выходящим траекториям, нужно двигаться точно с правильной скоростью. Но даже если ваша скорость будет чуть отличаться от правильной, вы все же сможете держаться вблизи нужных вам траекторий. Чтобы спланировать эффективный план полета, нужно первым делом решить, какие именно трубки могут представлять для вас интерес. Вы направляете аппарат по первой входящей трубке, а когда он достигает точки Лагранжа, короткий импульс двигателей перенаправляет его в определенную выходящую трубку. Со временем она перетекает в другую входящую трубку… и т. д.
В 2000 году Вансан Кунь, Мартин Лоу, Джеррольд Марсден и Шейн Росс использовали трубки для планирования облета лун Юпитера, с гравитационным маневром у Ганимеда и затем перелетом по трубке к Европе. Более сложный маршрут, требующий даже меньше энергии, включает еще и Каллисто. В нем используется динамика пяти тел: Юпитера, трех его лун и самого космического аппарата.
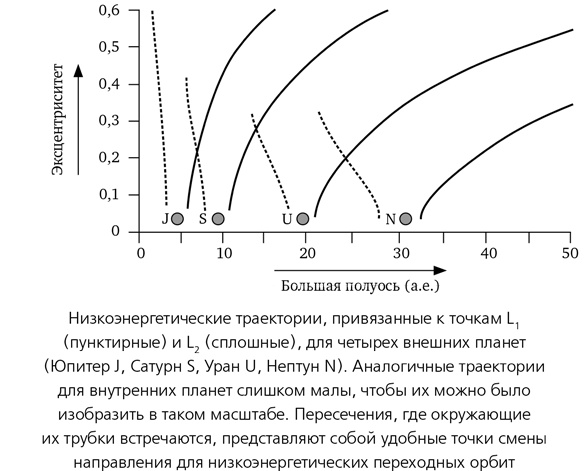
В 2002 году Лоу и Росс просчитали естественные пути в энергетическом ландшафте, ведущие в точки L1 и L2 планет Солнечной системы и из них, и обнаружили, что они пересекаются друг с другом. Рисунок иллюстрирует эти траектории в одном из сечений Пуанкаре. Пунктирная кривая линия, выходящая из Сатурна (S), пересекает сплошную линию, выходящую из Юпитера (J), задавая тем самым низкоэнергетическую переходную траекторию между двумя этими планетами. То же можно сказать и о других пересечениях. Таким образом, стартовав от Нептуна, космический аппарат может эффективно переместиться к Урану, затем к Сатурну, потом к Юпитеру, переключаясь у каждой планеты между точками L1 и L2. Тот же процесс можно продолжить и дальше, к внутренним планетам Солнечной системы, или, наоборот, вовне, шаг за шагом. Это и есть математическая основа, можно сказать, скелет межпланетных автострад.




