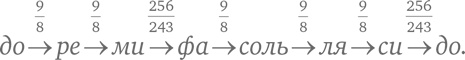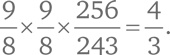Складывать и вычитать отрезки просто. Пусть у нас есть отрезки длиной a и b. С помощью линейки мы продлеваем первый отрезок. Ставим иглу циркуля в начало второго отрезка, а острие карандаша на другой ножке циркуля – в конец отрезка. После этого мы перемещаем иглу в конец первого отрезка и отмечаем точку на продленной линии. Так мы находим сумму двух отрезков. Что касается вычитания, оно будет означать не приращение, а укорочение отрезков.
Дальше дело пойдет несколько сложнее, но мы вполне способны умножать, делить и даже извлекать квадратные корни из длин отрезков с помощью линейки без делений и циркуля.
Да, это так: с помощью двух простейших инструментов мы можем найти длины, равные всем положительным конструктивным числам!
Было время, когда греки думали, что все числа рациональные, но пифагорейцы доказали, что это не так.
Однако грекам было непросто расстаться с верой в связь арифметики и геометрии. В основе этой веры лежали представления об эстетике. Неужели не все числа можно выразить с помощью линейки без делений и циркуля?
Эта вера подкреплялась решениями двух из трех знаменитых древнегреческих геометрических задач. Наиболее известна задача о трисекции угла: с помощью линейки без делений и циркуля нужно поделить заданный угол на три равных угла
[45].
Менее известны две другие головоломки:
• Удвоение куба. Необходимо найти длину ребра куба, чей объем в два раза больше заданного. Если длина ребра первого куба – единица, это равносильно построению отрезка длиной
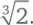
• Квадратура круга. Необходимо построить квадрат, чья площадь равна площади заданного круга. Если радиус круга равен единице, его площадь равна π. Тогда сторона квадрата будет равна

Понадобилось две тысячи лет, чтобы понять: эти задачи неразрешимы
[46]. Ни
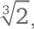 ни
ни
 не являются конструктивными числами
[47]. Решая проблему трисекции угла, мы сталкиваемся с тем фактом, что некоторая величина (косинус 20°) не является конструктивным числом.
не являются конструктивными числами
[47]. Решая проблему трисекции угла, мы сталкиваемся с тем фактом, что некоторая величина (косинус 20°) не является конструктивным числом.
Существование неконструктивных чисел опровергает связь между арифметикой и геометрией, гревшую сердца древним грекам, которые решали задачи на построение с линейкой без делений и циркулем.
Музыкальная гармония
Если музыканты перед концертом не настроили инструменты, возникает акустический диссонанс: музыка становится неблагозвучной.
Когда на двух инструментах берут одинаковые ноты, акустическая частота звуковых волн оказывается одинаковой. Рассогласованность же действует слушателю на нервы. Впрочем, можно брать и разные ноты, и музыка все равно будет ласкать слух, если эти ноты гармонируют друг с другом. Но как достичь гармонии? Что именно нам приятно слышать?
Этот вопрос волновал еще древних греков. Они выяснили, что, если акустические частоты соотносятся как малые целые числа (например, 2 и 3), сочетание нот ласкает слух. Так был открыт первый музыкальный строй (по легенде, его создал Пифагор
[48]). Подбирая частоты для нот, важно выполнить главное требование: частоты нот, находящихся на противоположных концах октавы, должны соотноситься примерно как 2:1. Ради гармоничных звуков древние греки подбирали ноты так, чтобы парное соотношение частот до и фа, а также до и соль выражалось малыми целыми числами. В пифагорейском варианте соотношение между частотами соседних нот было равно 9/8 для целого тона (например, между до и ре) и 256/243 для полутона (например, между ми и фа).
Вот весь пифагоров строй
[49]:
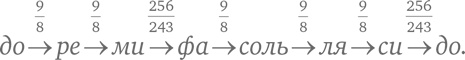
Из этого соотношения можно посчитать соотношение, скажем, между частотами нот до и фа. Мы получим частоту фа, если умножим частоту до на
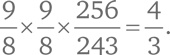
Акустические частоты, соотносящиеся как 4:3, прекрасно звучат вместе.
Мы можем визуализировать звуковые волны, возникающие, когда до и фа звучат вместе. Это будет выглядеть примерно так:

А частота ноты ля окажется немножко выше, звуковая волна будет выглядеть так:

Разница, заметная для глаза, заметна также и для слуха; вы видите диссонанс.
Недостаток пифагорова строя в том, что широко распространенное мажорное трезвучие до мажор – до-ми-соль – звучит как диссонанс; соотношение частот достаточно сложное.
Спустя много веков были найдены другие варианты. Например, так называемый чистый строй, или натуральный строй
[50], выглядит так:



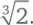

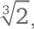 ни
ни
 не являются конструктивными числами
не являются конструктивными числами