А что, если вам и этого мало? Что, если вы потребуете от банка платить вам ежечасно?.. ежеминутно?.. ежесекундно?
В году 31 556 926 секунд
[73], так что спустя 10 лет у вас будет:
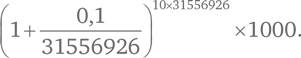
Это дает 2718,28 доллара.
Подытожим:
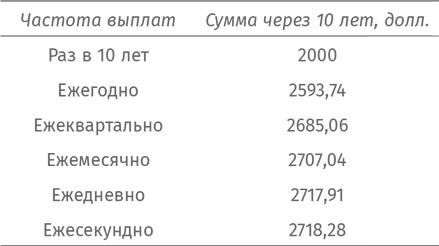
А зачем останавливаться на секундах? Пусть банк выплачивает вам деньги каждую миллисекунду или наносекунду. Впрочем, это не изменит общей суммы. Вы все равно получите те же 2718,28 доллара, потому что вынуждены округлять до центов.
В пределе вы достигнете непрерывных выплат. Если посчитать всю сумму в точности, банк должен будет отдать вам 1000 × e долларов!
Непрерывные выплаты – пример экспоненциального роста. Пусть A – начальное число (денег, микробов и т. д.). Оно вырастает со скоростью r на протяжении периода времени t. Если новое число вырастает с той же скоростью и этот рост непрерывный, то в конце мы получим:
где e – знакомое нам число Эйлера. В нашем примере A = 1000 (первоначальный вклад), r = 0,1 (процентная ставка), t = 10 (количество лет). В конце мы имеем 2718,28 доллара.
Процесс может быть и обратным, когда нечто непрерывно убывает
[74]. Тогда в конце мы получим Ae–rt.
Переполох со шляпами
В одном городе был театр. Его посетители на время представления сдавали шляпы в гардероб, а потом забирали обратно.
Однажды гардеробщик – то ли он выпил лишнего, то ли просто свихнулся – стал выдавать шляпы не по номеркам, а в произвольном порядке. Вопрос: какова вероятность того, что никто не получит свою шляпу?
Сформулируем вопрос точнее. В театр пришло N зрителей. Они встают в очередь за шляпами. Сумасшедший гардеробщик выдает шляпы в произвольном порядке. Таким образом, шляпы могут быть выданы N! различными вариантами
[75]. Все они равновероятны. Это математическая формулировка выражения «в произвольном порядке».
Разберем случай N = 4. Укажем в таблице все варианты выдачи шляп и пометим стрелочкой те случаи, когда ни один из зрителей не получает свою шляпу.
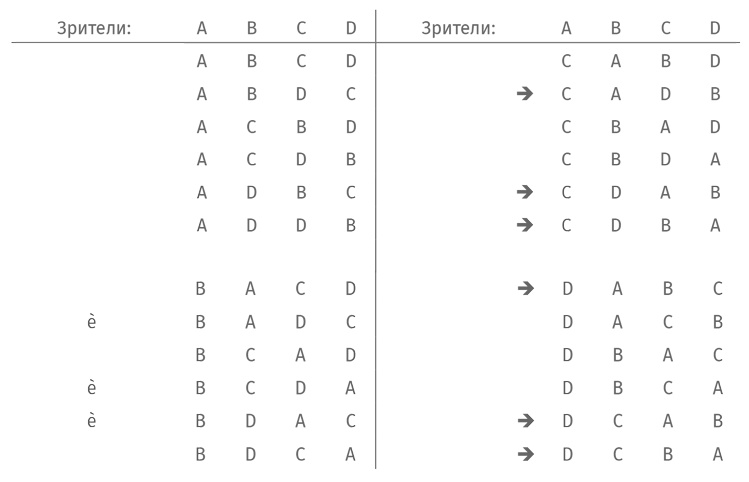
В 9 случаях из 24 никто не получает свою шляпу. Таким образом, при N = 4 интересующая нас вероятность равна
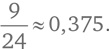
Для N = 5 существует 5! = 120 различных вариантов вернуть шляпы. Из них 44 нам подходят: ни один человек не получит свою шляпу. Таким образом, вероятность будет равна
 В таблице вы можете видеть, как меняется вероятность по мере возрастания N.
В таблице вы можете видеть, как меняется вероятность по мере возрастания N.
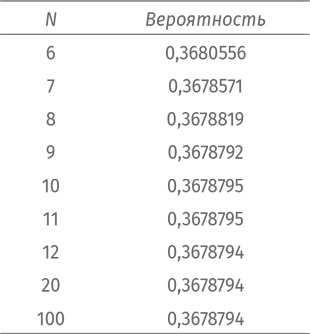
Вероятность меняется и дальше, но на ничтожно малую величину.
Хорошенько подумав, мы можем вывести формулу зависимости вероятности того, что никто из N зрителей не получит свою шляпу, от числа N:
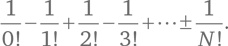
Например, при N = 4
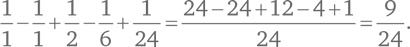
Это согласуется с нашими предыдущими выкладками.
В пределе, когда N стремится к бесконечности, вероятность того, что никто не получит свою шляпу, равна

Этот ряд уходит в бесконечность. Обратите внимание, что эта формула похожа на формулу (A) для подсчета числа e. Сумма ряда (B) равна
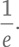 Мы снова встретили наше заветное число!
Мы снова встретили наше заветное число!
Уже при N = 10 сумма ряда будет равна

Это достаточно близко к следующему значению:

Среднее расстояние между двумя простыми числами
В главе 1 я доказал, что простых чисел бесконечно много. Вы увидели, что среди небольших целых положительных чисел простые числа встречаются достаточно часто, но, когда мы уходим в бесконечность, простые числа начинают попадаться все реже. Мы можем с некоторой точностью установить, насколько редко встречаются простые числа, если попытаемся найти среднее расстояние между ними
[76].



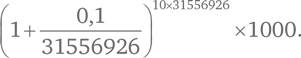


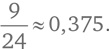
 В таблице вы можете видеть, как меняется вероятность по мере возрастания N.
В таблице вы можете видеть, как меняется вероятность по мере возрастания N.
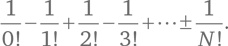
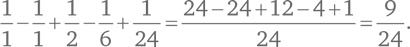

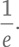 Мы снова встретили наше заветное число!
Мы снова встретили наше заветное число!
