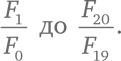А вот совершенно другое доказательство тождества (*). Основной подход тут – воспользоваться тем фактом, что число Fn – это количество способов облицевать прямоугольник 1 × n квадратами и костяшками домино.
Напомню, что нам нужно доказать:
F0 + F1 + F2 + … + Fn = Fn + 2– 1. (*)
Идея заключается в том, чтобы рассматривать обе части уравнения как решение задачи с облицовкой. Если мы докажем, что левая и правая часть – решение для одного и того же прямоугольника, они совпадут между собой. Эта техника носит название комбинаторного доказательства
[97].
На какой вопрос по комбинаторике уравнение (*) дает два верных ответа? Эта головоломка похожа на те, что встречаются в шоу Jeopardy!
[98], где участники должны формулировать вопрос, заранее зная правильный ответ.
Правая часть выглядит проще, поэтому начнем с нее. Ответ: Fn + 2 – 1. Каков вопрос? Если бы ответ был равен просто Fn + 2, мы с легкостью сформулировали бы вопрос: сколькими способами можно облицевать прямоугольник 1 × (n + 2) с помощью квадратов и костяшек домино?
Это почти то, что нужно, но ответ меньше на единицу. Попробуем мягко поменять вопрос и уменьшить ответ. Уберем один вариант облицовки и пересчитаем оставшиеся. Сложность состоит в том, чтобы найти один вариант, который кардинально отличается от остальных. Есть ли такой?
Каждый способ облицовки подразумевает использование квадратов и/или домино. Только квадраты задействованы в единственном варианте, в прочих есть хотя бы одна костяшка домино. Возьмем это за основу нового вопроса.
Вопрос: Сколько существует вариантов облицовки квадратами и костяшками домино прямоугольной рамки 1 × (n + 2), включающих по меньшей мере одну костяшку домино?
Сейчас мы найдем два ответа на этот вопрос. Так как оба будут верны, между числами мы сможем уверенно поставить знак равенства.
Один из ответов мы уже обсуждали. Есть Fn + 2 вариантов укладки. Только один из них подразумевает использование исключительно квадратов, без домино.
Таким образом, ответ № 1 на наш вопрос таков: Fn + 2 – 1.
Второй ответ должен быть – я надеюсь – левой частью уравнения (*). Посмотрим, как это работает.
Нужно пересчитать варианты заполнения рамки, включающие хотя бы одну костяшку домино. Давайте подумаем, где будет расположена самая первая костяшка. Есть n + 2 позиций, и первая костяшка может располагаться в позициях от 1 до n + 1.
Рассмотрим случай n = 4. Мы ищем варианты заполнения рамки 1 × 6, задействующие хотя бы одну костяшку домино. Мы знаем ответ: F6 – 1 = 13 – 1 = 12, но нам необходимо получить его иным путем.
Первая костяшка домино может занимать следующие позиции:
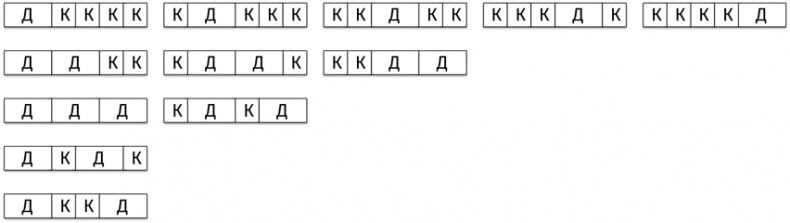
Первая колонка демонстрирует случай, когда костяшка находится на первой позиции, вторая – когда костяшка на второй, и т. д.
Сколько вариантов в каждой колонке?
В первой колонке – пять вариантов. Если отбросить домино слева, мы получим ровно F4 = 5 вариантов для прямоугольника 1 × 4.
Во второй колонке – три варианта. Отбросим домино и квадрат слева. Мы получим F3 = 3 варианта для прямоугольника 1 × 3.
Аналогично для других колонок. Вот что мы обнаружили:
Таким образом, количество способов замостить квадратами и домино (хотя бы одной костяшкой) прямоугольную рамку 1 × 6 равно
F4 + F3 + F2 + F1 + F0 = 12.
Вывод:
F0 + F1 + F2 + F3 + F4 = 12 = F6 – 1.
Рассмотрим общий случай. Нам дана рамка длиной n + 2. Сколько есть вариантов ее заполнения, при которых первая костяшка домино находится на некой позиции k? В этом случае первые k – 1 позиций заняты квадратами. Таким образом, в общей сложности занята k + 1 позиция
[99]. Оставшиеся (n + 2) – (k + 1) = n – k + 1 можно заполнить любыми способами. Это дает Fn – k + 1 вариантов. Построим диаграмму:
Если k меняется от 1 до n + 1, величина n – k + 1 меняется от 0 до n. Таким образом, количество вариантов заполнения нашей рамки с использованием хотя бы одной костяшки домино равно
Fn + Fn – 1 + … + F1 + F0.
Если поставить слагаемые в обратном порядке, мы получим левую часть выражения (*). Таким образом, мы нашли второй ответ на поставленный вопрос:
Итак, у нас есть два ответа на вопрос. Величины, полученные с помощью двух выведенных нами формул, совпадают, и тождество (*) доказано.
Соотношение чисел Фибоначчи и золотое сечение
Сложение двух следующих друг за другом чисел Фибоначчи дает очередное число Фибоначчи. В этом разделе мы затронем вопрос поинтереснее: что будет, если мы поделим число Фибоначчи на предшествующее ему в ряду? Посчитаем соотношение
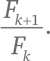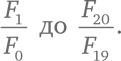
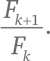Для возрастающих значений k. В таблице вы можете видеть соотношения от
