Еще одна пифагорова тройка: 33, 56, 65.
Я продемонстрировал процедуру поиска пифагоровых троек. Возникает естественный вопрос: все ли пифагоровы тройки можно найти подобным образом? Да, но доказательство этого факта довольно сложное, так что, если вам интересно, я рекомендую обратиться к литературе по теории чисел.
Великая теорема Ферма
Мы рассмотрели тройки целых чисел, удовлетворяющих уравнению теоремы Пифагора. Они лишь косвенным образом связаны с миром прямоугольных треугольников. Сейчас мы полностью перенесемся за пределы геометрии и подумаем о решениях уравнения aⁿ + bⁿ = cⁿ.
Легко найти тройки целых чисел a, b, c, удовлетворяющих соотношению a + b = c. В предыдущем разделе я рассказал о способе поиска троек целых чисел, удовлетворяющих уравнению a² + b² = c². Сейчас нам предстоит перейти к более высоким степеням: можем ли мы найти тройки целых чисел, удовлетворяющих уравнению a³ + b³ = c³, или a⁴ + b⁴ = c⁴, или a⁵ + b⁵ = c⁵ и т. д.?
Вот два неинтересных решения уравнения a³ + b³ = c³:
5³ + 0³ = 5³; 5³ +(–5)³ = 0³.
Куда сложнее найти тройки целых чисел, не равных нулю, которые являются решениями уравнения a³ + b³ = c³. Такие решения называются нетривиальными.
Этот вопрос в 1637 году заинтересовал Пьера Ферма. На полях «Арифметики» Диофанта он сформулировал следующее утверждение: уравнение aⁿ + bⁿ = cⁿ не имеет нетривиальных целочисленных решений при n ≥ 3. Он записал по-латыни знаменитые слова:
Невозможно разложить куб на два куба, биквадрат на два биквадрата и вообще никакую степень, большую квадрата, на две степени с тем же показателем. Я нашел этому поистине чудесное доказательство, но поля книги слишком узки для него
[158].
Это утверждение известно как великая теорема Ферма, хотя сомнительно, что Ферма мог доказать ее. Потребовалось три столетия, прежде чем Эндрю Уайлс
[159] нашел доказательство и опубликовал его в середине 1990-х. Он показал, что теорема Ферма верна и уравнение aⁿ + bⁿ = cⁿ не имеет нетривиальных целочисленных решений при n ≥ 3.
Глава 15
Окружности
Окружности изящны и красивы. Глава 15 содержит россыпь любопытных фактов об этих основополагающих геометрических фигурах.
Точное определение
Математики избегают туманных определений, им подавай точность! Окружность – это множество точек на плоскости, равноудаленных от некоторой точки
[160]. Давайте распутаем этот клубок.
Прежде всего, окружность представляет собой множество точек. Естественно, не любое множество точек образует окружность. Речь идет лишь об избранных точках. Избранных по какому принципу? Окружность – это множество точек, заданных двумя условиями: положительным числом r и точкой X. Как вы знаете, точку X мы называем центром окружности, а число r – радиусом.
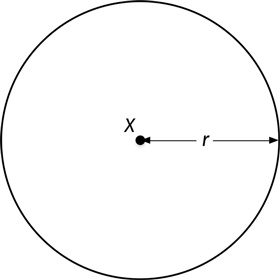
При построении (чернилами на бумаге или пикселями на экране) окружность имеет некоторую толщину, но с математической точки зрения толщина окружности равна нулю.
Окружности – близкие родственники сфер. А что такое сфера? Это множество точек в пространстве, равноудаленных от некоторой точки. Обратите внимание: два определения почти одинаковы, за исключением того, что окружность находится в плоскости.
Уравнение окружности
Точки на плоскости задаются двумя координатами: x и y. Если мы записываем уравнение с двумя переменными, множество точек, чьи координаты удовлетворяют этому уравнению, задают какую-нибудь геометрическую фигуру.
Например, уравнению x² + y² = 1 удовлетворяют некоторые, но не все точки плоскости. Скажем, точка с координатами (1, 0) удовлетворяет уравнению, потому что 1² + 0² = 1. Точно так же точка (3/5, 4/5) тоже удовлетворяет уравнению:
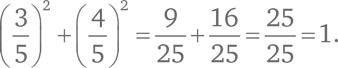
С другой стороны, точка (1/2, 1/2) не удовлетворяет уравнению, потому что
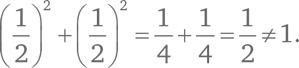
Что можно сказать о точках, удовлетворяющих уравнению x² + y² = 1? Они задают окружность с центром в начале координат и радиусом 1.
Почему? Давайте подумаем о точке (x, y). Она задает прямоугольный треугольник. Проведем перпендикуляры к осям абсцисс и ординат и соединим отрезком нашу точку с началом координат, как показано на рисунке.
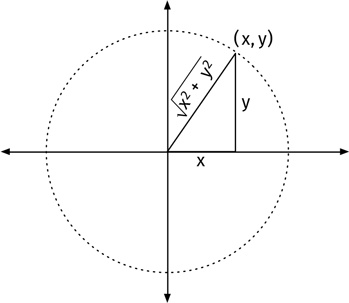
Длины катетов треугольника равны x и y, и по теореме Пифагора (см. главу 14) длина гипотенузы равна
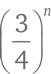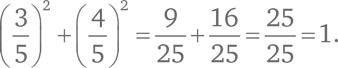
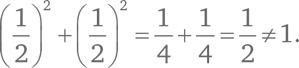
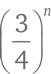Это не что иное, как расстояние от точки (x, y) до точки (0, 0).
