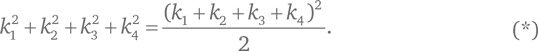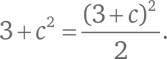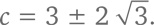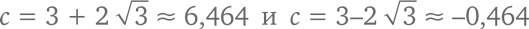Декарт пришел к следующему выводу: если кривизны «целующихся» окружностей равны k1, k2, k3, k4, то соотношение между ними укладывается в формулу:
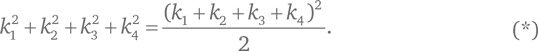
Например, если три большие окружности имеют радиус/кривизну 1, а кривизна малой окружности равна c, то из формулы (*) следует:
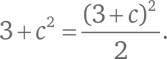
Решение квадратного уравнения дает
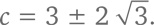
Таким образом,
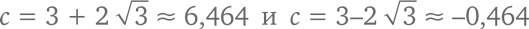
Отрицательное число нам не подходит, ведь как радиус/кривизна окружности может быть меньше нуля? Таким образом, кривизна малой окружности равна примерно 6,464, а радиус – примерно 0,1547.
Четыре окружности могут «поцеловаться» иначе. Начертим снова три окружности, касающиеся друг друга, но вместо малой окружности внутри опишем большую окружность, касающуюся всех трех окружностей снаружи:
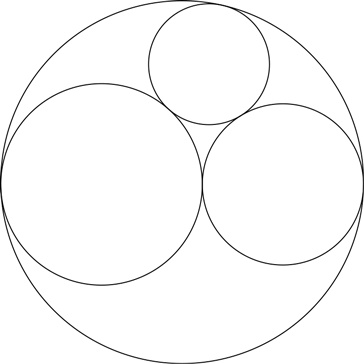
Хорошая новость: решение Декарта по-прежнему остается в силе. Фокус состоит в том, чтобы взять отрицательный корень квадратного уравнения с обратным знаком!
Например, давайте снова рассмотрим три окружности с радиусом 1. Формула (*) вновь приводит нас к двум ответам. Но теперь большая окружность имеет кривизну где-то 0,464 и радиус где-то 2,1547.
Иначе говоря, формула Декарта работает и в том случае, когда мы вычисляем радиус малой окружности внутри трех, касающихся друг друга, и в том случае, когда мы ищем радиус большой окружности, охватывающей эти три.
Если корень уравнения отрицательный, речь идет об описанной окружности; в случае положительного корня речь идет о вписанной окружности. А теперь другой вопрос: что означает нулевая кривизна? Сама формулировка подсказывает, что «окружность» с нулевой кривизной представляет собой прямую линию
[165].
Решение Декарта в 1930-е годы заново открыл Фредерик Содди
[166]. Он был настолько поражен элегантностью формулы, что сочинил стихотворение под названием «Прицельный поцелуй». Вот вторая строфа, где зарифмована формула (*):
Окружности четыре
Сошлись для поцелуя,
Пригожая малютка
Скривилась больше всех.
А если единичку
На радиус делю я,
То это будет кривизна.
Невиданный успех!
Евклид буквально онемел…
Дружок, скорей берись за мел:
Коль нулевая кривизна,
То линия прямая;
Коль минус перед кривизной,
Целуйся, обнимая.
«Сложи криви́зны, возведи
В квадрат всю эту сумму,
И на два ну-ка подели!» –
Кричу я тугодуму. –
«Теперь все это приравняй
К величине другой:
Криви́зны возведи в квадрат,
Сплюсуй, мой дорогой».
Две суммы в точности равны,
И все от радости пьяны:
Целуются, милуются,
Собой не налюбуются!
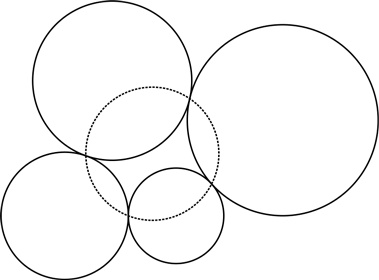
Есть еще один вариант поцелуя четырех окружностей. На сей раз они будут касаться друг друга попарно, выстроившись в кольцо. Иными словами, касаются первая и вторая окружности, вторая и третья, третья и четвертая, четвертая и первая. Итого мы имеем четыре точки соприкосновения.
Удивительно, но факт: эти четыре точки всегда будут лежать на другой окружности, пятой по счету.
Теорема Паскаля о шестиугольнике
Я завершу эту главу теоремой, доказанной Блезом Паскалем
[167].
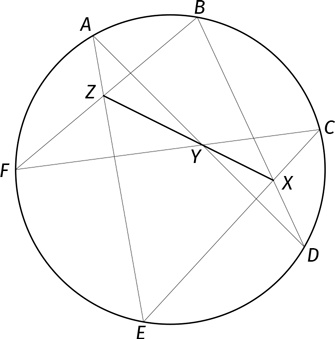
Расставим на окружности шесть точек: A, B, C, D, E и F. Соединим их отрезками, чтобы возник перекрученный шестиугольник:
A → D → B → F → C → E → A.
Теорема Паскаля говорит о том, что три точки, в которых пересекаются пары отрезков DB и CE, AD и FC, BF и EA (на чертеже они отмечены буквами X, Y, Z соответственно) всегда будут лежать на одной прямой!
Отмечу, что теорема Паскаля верна и в случае шести точек, лежащих на эллипсе
[168].
Плотность гексагональной упаковки кругов
Предположим, все круги имеют радиус 1. Центры четырех соседних кругов расположены на вершинах ромба со стороной 2.
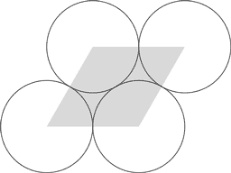
Ромб состоит из двух равносторонних треугольников. Высота равностороннего треугольника
[169] со стороной 2 равна √3. Таким образом, площадь треугольников равна

Площадь ромба вдвое больше: 2√3