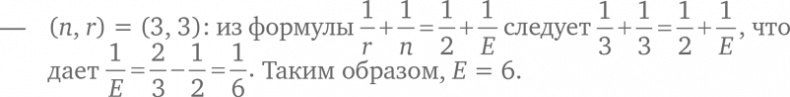V' = V – 1,
E' = E – 1,
F' = F = 1.
Таким образом, V' – E' + F' = (V – 1) – (E – 1) + F = V – E + F. Чему бы ни было равно число V – E + F, после уничтожения очередного листа и ребра оно останется прежним.
Сколько бы листов и соответствующих им ребер я ни стирал, замкнутых областей на рисунке не появится. Я буду выбирать новый лист, стирать его и соответствующее ребро и т. д. В конце концов на графе останется всего одна вершина. Но число V – E + F не поменяется.
Подведу итог. Я расплющил многогранник. Удалил ребра таким образом, чтобы замкнутые области не оставались изолированными друг от друга; в конце концов число замкнутых областей свелось к нулю; значения V, E и F менялись, но число V – E + F оставалось неизменным. Дальше я стал срывать листья и стирать соответствующие им ребра, пока не осталась одна-единственная уцелевшая вершина. И вновь значения V, E и F менялись, но число V – E + F прошло без потерь сквозь все катаклизмы. Итак, у меня есть одна вершина, одна область (ничем не ограниченное пространство вокруг этой вершины) и ни одного ребра. Иными словами, в финале моих деструктивных операций V = 1, E = 0, F = 1. Если я подставлю эти числа в формулу V – E + F, то получу 2. Так я подтвердил тождество (A) – формулу Эйлера для многогранников!
Есть там кто еще?
Мы познакомились с пятью правильными многогранниками: тетраэдром, кубом, октаэдром, додекаэдром и икосаэдром. С помощью формулы (A) я покажу, что других правильных многогранников не существует.
Я буду использовать пять букв для параметров правильного многогранника. Первые три вам хорошо знакомы: V – количество вершин, E – количество ребер и F – количество граней. Все грани правильного многогранника – правильные многоугольники; обозначим количество сторон каждой из граней буквой n. В каждой вершине сходится одинаковое число ребер; обозначим его буквой r.
Вот параметры для платоновых тел:
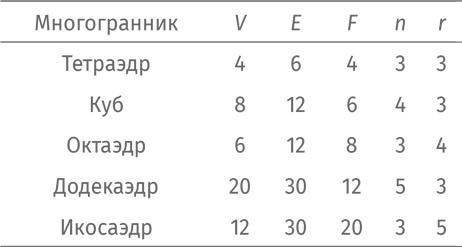
Давайте проработаем алгебраические взаимосвязи между этими числами.
Во-первых, напомню формулу Эйлера:
Во-вторых, мы будем использовать прием со штрихами, чтобы выяснить соотношение между E, V и r. Пометим штрихом оба конца каждого ребра. Общее количество штрихов – 2E. Кроме того, мы нанесем r штрихов возле каждой вершины, обозначив сходящиеся там ребра; всего у нас будет rV штрихов. Если все проделать аккуратно, оба числа совпадут:
В-третьих, выясним соотношение между E, F и n. Нам снова поможет прием со штрихами, но на сей раз мы станем наносить их, постепенно двигаясь по граням. Будем поочередно помечать штрихом ребра каждой грани. Как и раньше, на каждом ребре окажется по два штриха (так как оно отделяет две грани). Итак, с одной стороны, количество штрихов 2E, а с другой стороны, количество штрихов nF (n штрихов на каждой из F граней). Таким образом,
Давайте убедимся, что формулы (A), (B) и (C) верны для додекаэдра:
V – E + F = 20–30 + 12 = 2;
2E = 2 × 30 = 60 = 3 × 20 = rV;
2E = 2 × 30 = 60 = 5 × 12 = nF.
Сделаем еще кое-что.
Исходя из (B), мы имеем
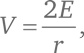 а исходя из (C), мы получаем
а исходя из (C), мы получаем
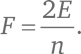 Подставим эти значения в формулу (A):
Подставим эти значения в формулу (A):
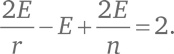
Поделим на 2E:
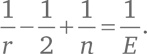
Прибавим к обеим частям 1/2:
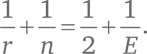
Эту формула нам скоро понадобится.
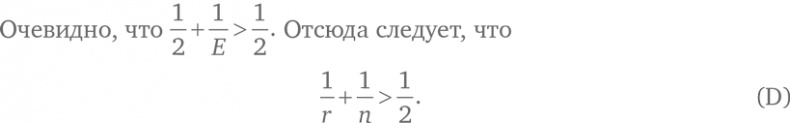
Соотношение (D) показывает, что r и n не могут быть слишком большими числами. Например, нет такой ситуации, при которой r = n = 5, потому что тогда
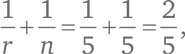 что не больше 1/2. Давайте подумаем над возможными значениями r и n.
что не больше 1/2. Давайте подумаем над возможными значениями r и n.
Вначале отметим, что r и n должны быть равны по меньшей мере 3. Грани – это многоугольники, и первая фигура в ряду n-угольников – треугольник. Многогранник – пространственная фигура; если r = 2, то в одной вершине встречаются всего два ребра; в случае с объемной фигурой необходимо r ≥ 3.
Переберем все возможные значения n:

Итак, есть всего 5 пар (n, r): (3, 3), (3, 4), (3, 5), (4, 3) и (5, 3).
Обладая значениями n и r, мы можем вычислить значение E (исходя из формулы
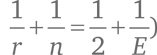 и затем вывести V и F, используя формулы (B) и (C). Вот выкладки для всех пяти случаев:
и затем вывести V и F, используя формулы (B) и (C). Вот выкладки для всех пяти случаев:
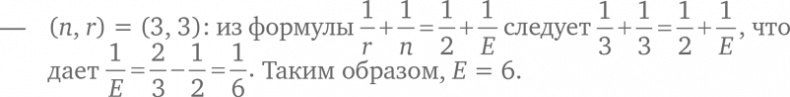
Исходя из (B), 2E = rV. Следовательно, 12 = 3V, и V = 4.
Исходя из (C), 2E = nF. Следовательно, 12 = 3F, и F = 4.




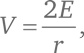 а исходя из (C), мы получаем
а исходя из (C), мы получаем
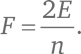 Подставим эти значения в формулу (A):
Подставим эти значения в формулу (A):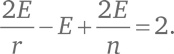
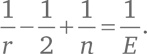
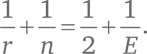
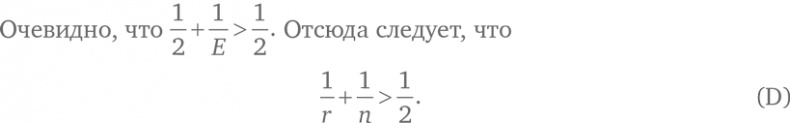
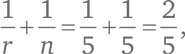 что не больше 1/2. Давайте подумаем над возможными значениями r и n.
что не больше 1/2. Давайте подумаем над возможными значениями r и n.
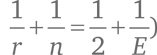 и затем вывести V и F, используя формулы (B) и (C). Вот выкладки для всех пяти случаев:
и затем вывести V и F, используя формулы (B) и (C). Вот выкладки для всех пяти случаев: