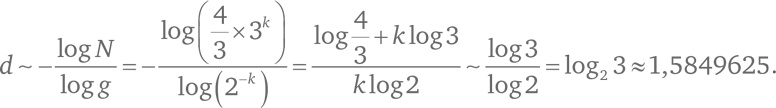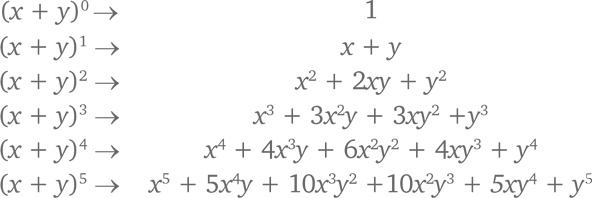Мы можем в точности вычислить размерность треугольника Серпинского, но это потребует базовых знаний о логарифмах и некоторых алгебраических выкладок. Если вам все это в тягость, можете спокойно пропустить следующие абзацы.
Итак, цель состоит в том, чтобы найти формулу вроде (A) или (B):
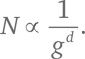 Число d в ней и будет количеством измерений нашей фигуры.
Число d в ней и будет количеством измерений нашей фигуры.
Если сторона клеточки равна
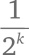 (где k – натуральное число), то
(где k – натуральное число), то
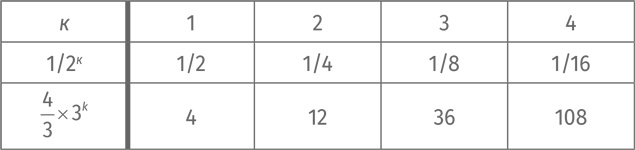
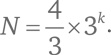 Вот проверка:
Вот проверка:
Формула
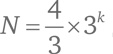 дает в точности те же числа, что и в предыдущей таблице.
дает в точности те же числа, что и в предыдущей таблице.
Задача состоит в том, чтобы найти такое число d, что
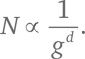 Прологарифмируем обе части
[185]:
Прологарифмируем обе части
[185]:
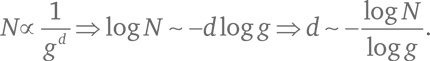
Мы знаем
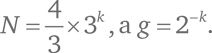 Подстановка в предыдущую формулу дает:
Подстановка в предыдущую формулу дает:
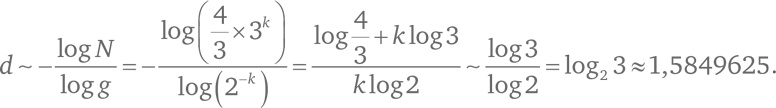
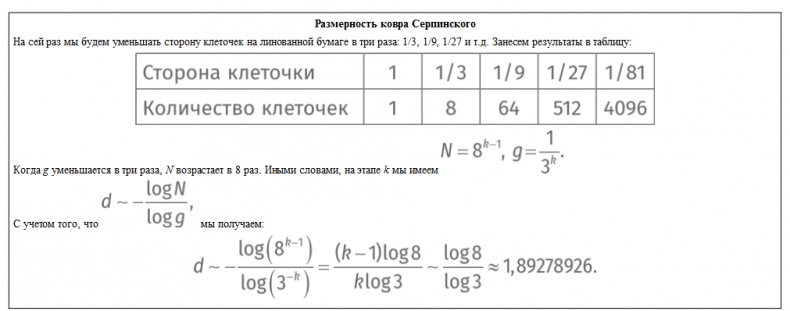
Наряду с треугольником Серпинского существует ковер Серпинского. Вот этапы его построения:
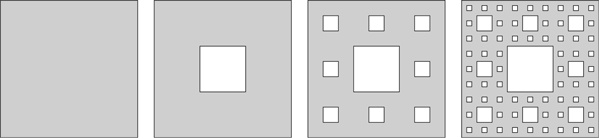
Устремляясь к бесконечности, мы получим такую картинку:

Как вы думаете, какова размерность этого фрактала? Ответ вы найдете в конце главы.
Серпинский и Паскаль
Студенты на факультетах математики до потери пульса разлагают на множители полиномы, в первую очередь степени x + y. Восстановим в памяти, о чем идет речь:
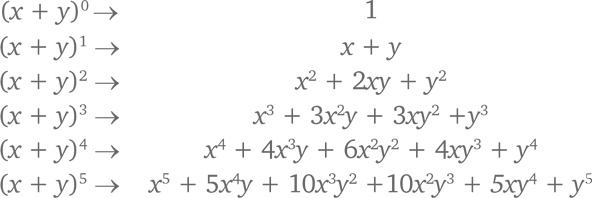
Мы можем расположить коэффициенты данных полиномов в таблице. Ее называют треугольником Паскаля:
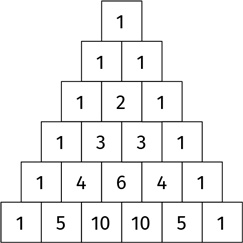
Мы расположили эти числа по квадратам, а теперь давайте раскрасим некоторые из них черным цветом. Пусть квадраты с нечетными числами станут черными, а квадраты с четными останутся белыми:
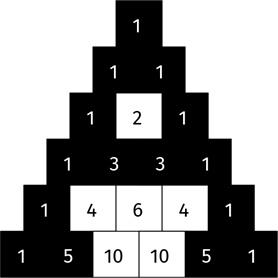
Продолжим вплоть до 64 ряда. Как вы думаете, что получится?

Разве это не великолепно?
Снежинка Коха
Я хочу завершить главу, посвященную фракталам, рассказом о неотразимой фигуре, придуманной Хельге фон Кохом
[186]. Алгоритм ее построения чрезвычайно прост. Мы начинаем с прямого отрезка, делим его на три части и строим равносторонний треугольник на основе среднего из трех новых отрезков. Затем мы удаляем центральный отрезок. Теперь у нас есть четыре отрезка, каждый из которых в три раза меньше исходного. Мы повторяем процедуру с каждым из этих отрезков.
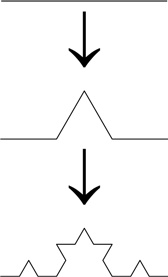
Чтобы получить снежинку целиком, начнем с равностороннего треугольника и проделаем описанную процедуру с каждой из его сторон. Это выглядит следующим образом:
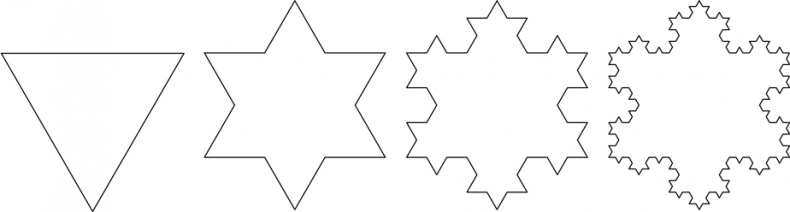
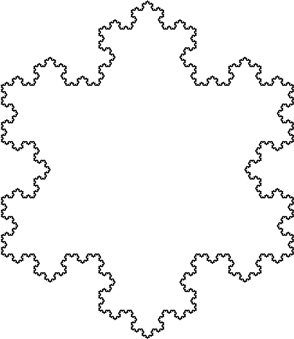
Устремляясь к бесконечности, мы получим снежинку Коха.
Глава 18
Гиперболическая геометрия
Постулаты Евклида
Математики помешаны на определениях. Мы требуем, чтобы все концепции базировались на кристально ясных, недвусмысленных определениях. Потому любая математическая идея основана на более простых идеях. Треугольник состоит из отрезков. Рациональные числа – это отношения целых чисел.
Спускаясь с башни математических определений, рано или поздно мы дойдем до фундамента. Для греков в основании всего лежала геометрия
[187].
Евклид не пытался дать определения базовым геометрическим объектам – точке, прямой линии, плоскости
[188]. Он поступил иначе: принял за данность определенные фундаментальные свойства, которыми обладают эти объекты. Тезисы Евклида называют постулатами, или аксиомами.



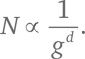 Число d в ней и будет количеством измерений нашей фигуры.
Число d в ней и будет количеством измерений нашей фигуры.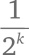 (где k – натуральное число), то
(где k – натуральное число), то
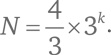 Вот проверка:
Вот проверка:
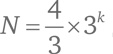 дает в точности те же числа, что и в предыдущей таблице.
дает в точности те же числа, что и в предыдущей таблице.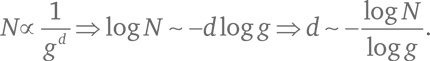
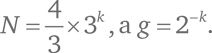 Подстановка в предыдущую формулу дает:
Подстановка в предыдущую формулу дает: