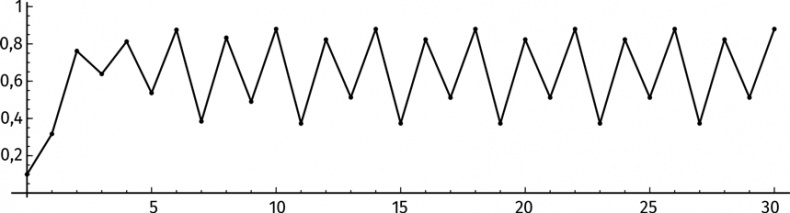
А вот таблица итераций:
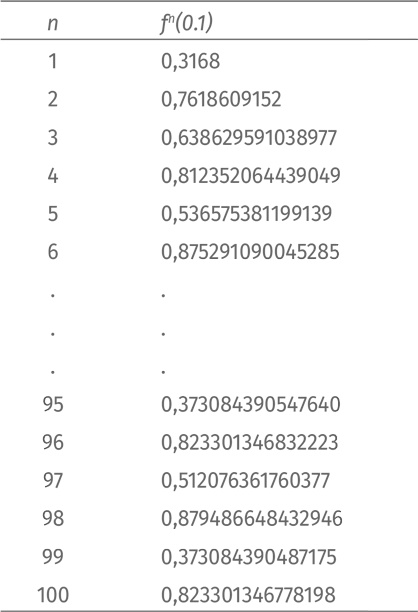
Долгосрочное поведение функции занятно, но по-прежнему стабильно. Система идет по циклу из четырех величин ad infinitum, как показано на иллюстрации.
От порядка к хаосу
Мы проследили долгосрочное поведение итераций логистического отображения f(x) = m x (1 – x). Итерации всегда приводили нас к стабильности. В некоторых случаях (m = 2,5 и m = 2,8) система сходилась к одной величине: неподвижной точке функции f. В других случаях (m = 3,2 и m = 3,52) она приобретала стабильный, предсказуемый ритм.
Жизнь хороша. Мы знаем исходную величину: x = 0,1. И мы знаем правило, по которому переходим от одного шага к другому: f(x) = m x (1 – x). Разумеется, мы можем предвидеть поведение функции на любом шаге до бесконечности. Верно?
Настало время для последнего примера: m = 3,9. Доверим подсчет первых 10 итераций компьютеру:
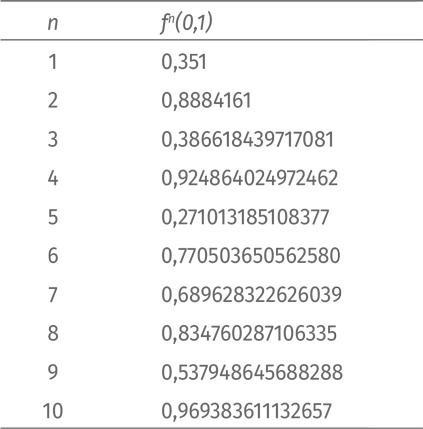
Что происходит? Неясно. Попробуем изобразить на графике первые 30 итераций:
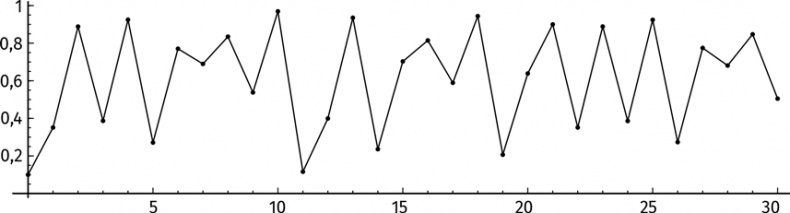
Хм… Ритм не прослеживается. Спокойствие, только спокойствие! Изобразим на графике первые 100 итераций.
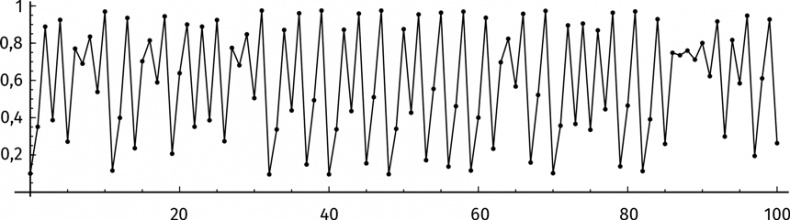
Колебания величин выглядят случайными. Разумеется, на самом деле это не так! Значение функции на каждом шаге можно точно подсчитать по формуле f(x) = 3,9 x (1 – x). Но итерации логистического отображения никогда не приведут к стабильности. Хаос будет длиться вечно.
Великолепно: итерации беспорядочны, но система предсказуема на 100 %!
• Мы знаем исходную величину: x = 0,1.
• Мы знаем правило перехода от одного шага к другому: x → f(x) = 3,9 x (1 – x).
Следовательно, мы можем вычислить состояние системы, скажем, на тысячной итерации. Верно?
Неверно.
Мы загнаны в угол стечением двух обстоятельств: ошибок округления и чувствительности системы к исходному состоянию. Обсудим каждое из них.
Когда мы проводим вычисления на калькуляторе или на компьютере, результат зачастую оказывается приблизительным. Например, если мы делим 1 на 3, наши приборы выдают десятичную дробь 0,3333333. В ней, скажем, семь знаков после запятой. На самом деле троек после запятой бесконечно много, но калькулятор ограничивается конечным количеством цифр. После нескольких итераций функции f(x) = 3,9 x (1 – x) количество знаков после запятой достигает дюжины. Рано или поздно компьютер выдает лишь приблизительный, а не точный результат. Обычно мы не придаем значения таким ошибкам. Если мы подсчитываем, сколько картин уместится на пустой стене, нас не волнует ошибка на одну триллионную. Почему ошибки округления имеют значение в данном случае?
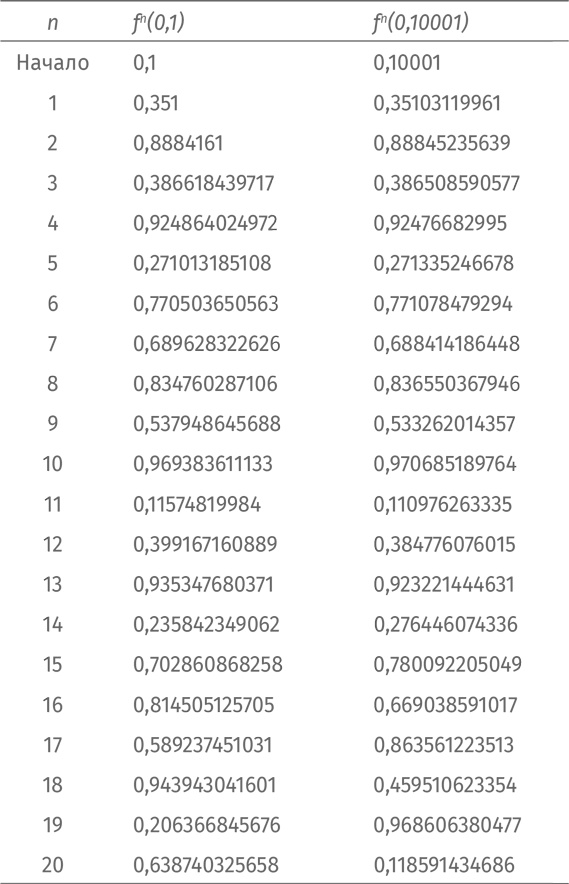
Они ведут нас к загвоздке – чувствительности системы к исходному состоянию. Посчитаем итерации нашей функции, начиная с двух почти что равных величин: х = 0,1 и х = 0,10001. Интуитивно мы предполагаем, что скромная разница между исходными величинами не играет роли. Так ли это? Что произойдет?
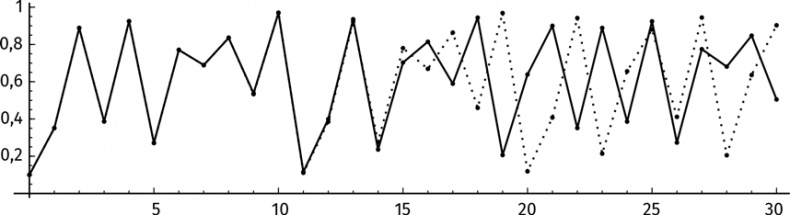
Замечу, что первые десять итераций или около того не приводят к значительным отличиям. Но затем траектории начинают расходиться. Это можно проиллюстрировать на графиках эволюции той и другой системы. Сплошная линия соответствует итерированию системы с исходным значением 0,1. Пунктирная линия иллюстрирует итерирование системы с исходным значением 0,10001.
Каково значение f1000 (0,1)? К чему мы придем, если мы проделаем тысячу итераций функции f(x) = 3,9 x (1 – x)?
Разумеется, мы доверяем вычисления компьютеру, но получается какая-то чепуха. Проиллюстрируем этот факт, проделав вычисления трижды с разным уровнем точности (заданным количеством знаков после запятой). Мы получим следующие результаты:

Ни одна из этих величин не равна f 1000 (0,1) в точности.
Мы будем биться до последней капли крови. Компьютер может работать с произвольной точностью. Он может не округлять полученное значение. К чему это приведет?
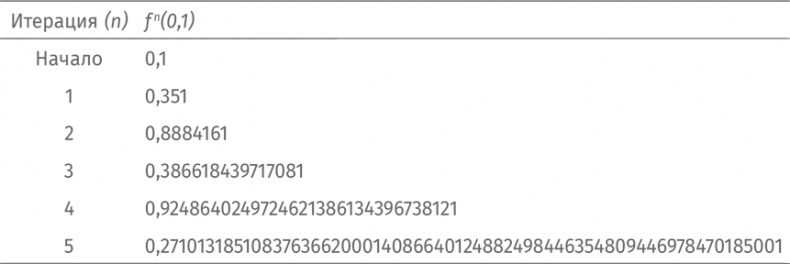
Точное значение f ⁶ (0,1) имеет длину 127 знаков после запятой, а точное значение f ⁷ (0,1) растягивается после запятой на 255 знаков. Количество знаков после запятой увеличится примерно вдвое на каждой итерации. Нет настолько мощного компьютера, чтобы вычислить точное значение f1000 (0,1).
К чему мы пришли? Несмотря на то что мы знаем исходное состояние системы и правило перехода от одного шага к другому, мы не в силах в точности предугадать ее состояние на 1000-м шаге.
Можно доказать, что точное значение f1000 (0,1) лежит между 0 и 1, и задаться вопросом: какова вероятность того, что f1000 (0,1), скажем, больше 0,5?
Ответ: либо 0, либо 1, потому что здесь нет ничего случайного. Либо f1000 (0,1) > 0,5, либо f1000 (0,1) ≤ 0,5, третьего не дано. Никаких «может быть», ничего случайного.
Даже настолько простая система способна оказаться хаотичной. Она абсолютно детерминирована и в то же время непредсказуема.












