Противоречие возникает в исходной постановке задачи, когда мы понимаем, что система должна одновременно иметь два противоположных свойства.
Простые примеры.
• Учебники должны быть маленькими (легкими), чтобы детям было удобно их носить, и большими (тяжелыми), чтобы вместить всю нужную информацию.
• Избыток ресурсов (площади, оборудование, техника, материалы) – это хорошо, так как не будет очередей, простоя работников, не потребуется сложной логистики… и плохо, поскольку повышает затраты. При недостатке ресурсов – всё наоборот.
• Персональные данные надо собирать, чтобы лучше узнать запросы клиентов, и нельзя собирать, потому что тем самым нарушается закон о конфиденциальности информации.
Когда противоречие разрешено, когда найдено сильное решение, это выглядит как волшебство.
Например, посетители первых небоскребов сталкивались с одним неприятным, но совершенно неизбежным физическим эффектом. В небоскребах лифтовые вентиляционные шахты, лестничные колодцы действовали как гигантские вытяжные трубы, создавая мощные воздушные потоки. Мощная тяга не давала открыть двери и окна
[10].
Противоречие: чтобы вихрей не было, двери должны быть всегда закрыты. Чтобы люди могли входить, двери должны быть открыты.
Первое, что, естественно, пришло в голову, – сделать воздушный шлюз (устройство, предназначенное для перемещения между зонами с разным давлением). В этом случае человек должен зайти в шлюзовую камеру, тщательно закрыть наружную дверь, открыть внутреннюю дверь и лишь затем войти. Для выхода эти операции нужно повторить в обратном порядке. Такое решение имеет множество недостатков: дорогая техническая система, долгая процедура прохождения, необходимость постоянного технического контроля шлюза, наличие риска человеческой ошибки. Дешево решить эту задачу не получалось.
Идеально было бы добиться того, чтобы одни двери сами закрывались, когда открываются другие.
Решение. 7 августа 1888 года Теофилус Ван Каннел получил американский патент № 387571 на изобретение «конструкции внешней двери». Ему удалось красиво разрешить противоречие: относительно воздуха дверь закрыта, относительно человека – открыта. Always Open, Always Closed (Всегда открыто, всегда закрыто).
Существуют три основных способа разрешения противоречий. (Попробуйте самостоятельно решить противоречия, приведенные ниже.)
1. Во времени
Формула: система в один момент времени имеет одно требуемое свойство, в другой момент – другое требуемое свойство.
Пример № 1. Одно из чудес света – Александрийский маяк на египетском берегу Средиземного моря. Несколько веков простоял маяк с надписью на стене: «Для богов и во имя спасения моряков построил Сострат из Книда, сын Дексифана». Так звали строителя, и люди запомнили его имя на века. Но история помнит и другое. Когда строительство маяка заканчивалось, Сострата вызвал правитель и повелел: «Ты выбьешь на плите мое имя!»
Строителю было запрещено высекать свое имя, и он знал, что, если он не выполнит приказ, его казнят, а если выполнит – потомки никогда не узнают, как звали настоящего создателя маяка. Строитель остался жив, но весь мир узнал его имя. Как это могло произойти?
Пример № 2. В 1804 году Наполеон Бонапарт пожелал принять титул императора для того, чтобы владеть, подобно своему кумиру Карлу Великому, огромной империей в Западной Европе. При этом, как и его знаменитый предшественник, он должен был быть коронован папой римским. В то же время его гордость, военное могущество и недоверие к папе не позволяли ему принять из его рук корону. Перед Бонапартом встала реальная проблема, в основе которой лежало столкновение двух противоположных желаний: быть и не быть коронованным. Как Наполеон разрешил противоречие?
2. В пространстве/структуре
Формула: в одном месте пространства объект обладает одним требуемым свойством, а в другом месте – другим требуемым свойством. Или: один элемент системы имеет одно требуемое свойство, а другой элемент системы – другое требуемое свойство.
Пример № 3. В тропических морях днища кораблей обрастают ракушками – до 45 кг/м²! Это тормозит ход корабля. Значит, надо днище чистить. Под воду лезет аквалангист, включает мотор круглой торцевой щетки и… закручивается в противоположную сторону сам – ведь опоры в воде нет. Как быть?
Опять нам встретилось противоречие: щетка должна крутиться, чтобы сдирать нарост, и не должна крутиться, поскольку это создает неудобство для работы. Как разрешить это противоречие во времени? Только коснулся щеткой днища – и сразу отвел. Аквалангист просто не успеет «закрутиться». Но так долго не поработаешь – утомительно.
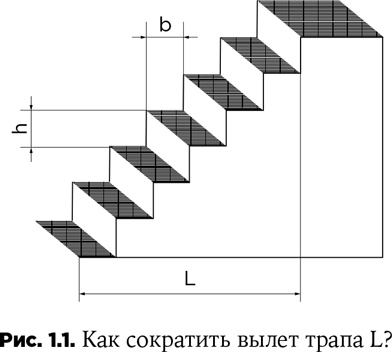
Пример № 4. На кораблях, особенно военных, каждый квадратный метр площади на счету. Особенно важно, чтобы любые сооружения занимали как можно меньше места. Но весьма трудно сократить вылет трапа, потому что он зависит от высоты и глубины ступенек. Сделать каждую ступеньку выше (тогда их потребуется меньше) нельзя: трудно ходить. А сделать каждую ступеньку у́же – тоже нельзя, так как на ней должна уместиться ступня (рис. 1.1).
3. В отношениях/воздействиях
Формула: относительно одного требования/воздействия объект обладает одним свойством, а относительно другого требования/воздействия – другим свойством.
Пример № 5. «– А ты слышал, как Петр Прокофьевич разместил в ангаре в два раза больше бомбардировщиков Ил-28, чем их можно было поместить туда теоретически? ‹…› О, это удивительная история. Понимаешь ли, если вычертить на картонке самолетики в масштабе и вырезать их, затем попытаться, комбинируя как угодно, разместить макетики на соответствующей в масштабе площади ангара, то могло получиться, что в самом лучшем случае в ангаре поместятся двенадцать самолетов… А тут у нас была как раз “полундра” с приемкой, требовались энергичные доработки многих машин, дело было то ли осенью, то ли зимой, и на открытом воздухе проделать это было невозможно. Словом, позарез требовалось установить побольше самолетов в ангар. И над этим у нас мудрили все, вплоть до начальника института. А тут прикатил сам министр, ходит злой – не подойти…
Да, кто-нибудь и сдрейфил бы, не подошел, только не Петр Прокофьевич! Он подошел к министру и говорит:
– Васильич, дашь на бригаду десять тысяч рублей – это было еще до денежной реформы, – если мы установим двадцать четыре Ила?..»
[11



