Хотя позже мир почти потерял Фибоначчи из виду, он, без сомнения, был выдающимся человеком своего времени. Его известность была настолько велика, что Фредерик II, сам ученый и исследователь, искал знакомства с ним и для этого организовал визит в Пизу. Фредерик II был императором Священной Римской империи, королем Сицилии и Иерусалима, потомком двух наизнатнейших семей Европы и Сицилии и самым влиятельным государем того времени. Он ратовал за абсолютную монархию и окружал себя пышностью, приличествующей императору.
Встреча Фибоначчи и Фредерика II произошла в 1225 г. и была весьма важным событием для Пизы. Император ехал во главе длинной процессии, состоящей из трубачей, придворных, рыцарей, чиновников и животных из императорского зверинца. Некоторые из проблем, поставленных императором перед великим математиком, рассмотрены в «Liber Abacci». По-видимому, Фибоначчи решил поставленные императором задачи, поскольку с тех пор всегда был желанным гостем при дворе. Когда в 1228 г. Фибоначчи подверг ревизии «Liber Abacci», он посвятил исправленное издание Фредерику II.
Будет почти преуменьшением сказать, что Леонардо Фибоначчи был величайшим математиком Средневековья. Его перу принадлежат три выдающихся математических труда: «Liber Abacci», опубликованная в 1202 и переизданная в 1228 г., «Practica Geometriae», изданная в 1220, и «Liber Quadratorium». Восхищенные граждане Пизы в 1240 г. подтвердили документально, что он был «благоразумным и ученым мужем», а совсем недавно Джозеф Гайз, старший редактор «Encyclopedia Britannica», заявил, что будущие исследователи со временем «воздадут должное Леонарду Пизанскому как одному из величайших в мире пионеров мысли». Его работы лишь теперь, спустя сотни лет, переведены с латыни на английский язык. Заинтересованные читатели могут обратиться к книге Дж. и Ф. Гайз «Леонард Пизанский и новая математика Средних веков», превосходному трактату, посвященному работам Фибоначчи и тем временам, когда они были написаны.
Несмотря на то что Фибоначчи был величайшим математиком Средневековья, его памяти посвящены лишь статуя, стоящая напротив Пизанской башни на другом берегу реки Арно, и две улицы, носящих его имя: одна в Пизе, а другая во Флоренции. Кажется странным, что среди несметных полчищ туристов, приходящих посмотреть на 179-футовую мраморную башню, лишь очень немногие хотя бы слышали имя Фибоначчи или видели его статую. Фибоначчи был современником Бонанны, архитектора, воздвигшего башню, строительство которой началось в 1174 г. Оба эти человека внесли свой вклад в мировую историю, но тот, чье влияние значительно превышало заслуги другого, остался почти неизвестным.
Последовательность Фибоначчи
В «Liber Abacci» поставлена задача, из решения которой возникает последовательность чисел 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 и так далее до бесконечности, сегодня известная как последовательность Фибоначчи. Задача формулируется следующим образом:
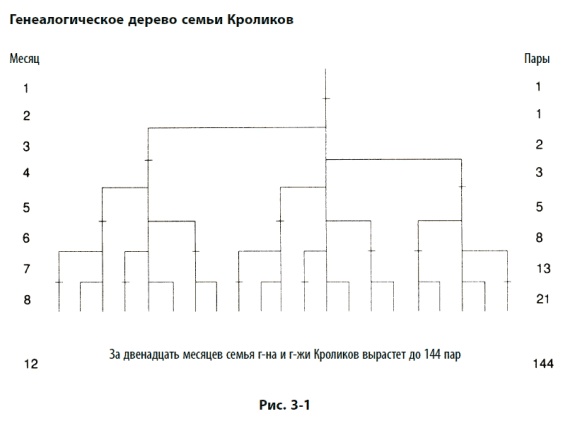
«Сколько пар кроликов, помещенных в закрытое пространство, можно получить за один год от одной пары кроликов, если каждая пара приносит каждый месяц, начиная со второго, новую пару?»
В поисках решения мы обнаруживаем, что каждой паре, включая первую, требуется месяц для созревания, но, начав плодиться, она приносит ежемесячно новую пару. К началу второго месяца у нас по-прежнему только одна пара. Таким образом возникает последовательность 1, 1. Эта первая пара в конце концов удваивает свое количество во время второго месяца, так что в начале третьего месяца имеется две пары кроликов. После этого старшая пара приносит третью пару в следующем месяце, так что в начале четвертого месяца последовательность расширяется до 1, 1, 2, 3. Из этих трех пар приносят потомство две старшие пары, а самая молодая – нет, и количество пар кроликов доходит до пяти. В следующем месяце потомство приносят три пары, а последовательность расширяется до 1, 1, 2, 3, 5, 8 и т. д. На рис. 3–1 показано древо популяции кроликов, где видно, что популяция растет с экспоненциальным ускорением. Если продолжать последовательность в течение нескольких следующих лет, цифры станут астрономическими. Через 10 месяцев, например, нам пришлось бы возиться с 3544224848179261915075 парами кроликов. Последовательность Фибоначчи, возникающая из задачки про кроликов, обладает многими интересными свойствами. Например, отношения между ее членами, находящимися на одинаковом расстоянии друг от друга, почти не изменяются.
Сумма любых двух соседних чисел последовательности равна следующему за ними члену: так, 1 плюс 1 равно 2, 1 плюс 2 равно 3, 2 плюс 3 равно 5, 3 плюс 5 равно 8 и так далее до бесконечности.
Золотое соотношение
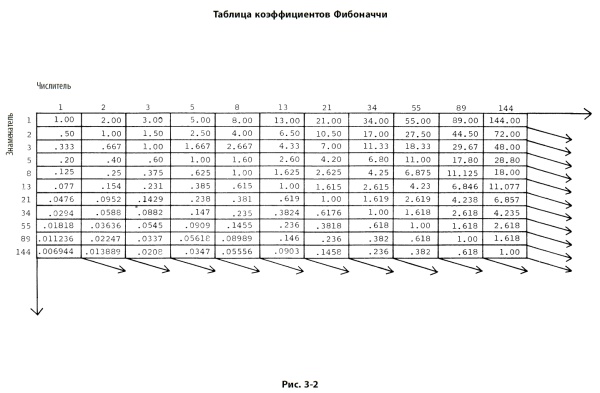
После нескольких первых чисел последовательности отношение любого ее члена к последующему приблизительно равно 0,618, а к предшествующему – 1,618. Чем больше порядковый номер члена последовательности, тем ближе отношение к числу фи (обозначается φ), являющемуся иррациональным числом и равному 0,618034… Отношение между членами последовательности, разделенными одним числом, примерно равно 0,382, а обратное ему число равно 2,618. На рис. 3–2 приведена таблица соотношений всех чисел Фибоначчи от 1 до 144.
φ является единственным числом, которое, будучи прибавленным к 1, дает обратное себе число: 1 + 0,618 = 1: 0,618. Это родство процедур сложения и умножения приводит к следующей последовательности уравнений:
0,6182 = 1–0,618
0,6183 = 0,618 – 0,6182
0,6184 = 0,6182 – 0,6183
0,6185 = 0,6183 – 0,6184
или
1,6182 = 1 + 0,618
1,6183 = 1,618 + 0,6182
1,6184 = 1,6182 + 0,6183
1,6185 = 1,6183 + 0,6184
Некоторые взаимосвязанные свойства этих четырех основных коэффициентов перечислены ниже:
1,618 – 0,618 = 1
1,618 × 0,618= 1
1 – 0,618 = 0,382
0,618 × 0,618 = 0,382
2,618 – 1,618 = 1
2,618 × 0,382= 1
2,618 × 0,618= 1,618
1,618 × 1,618 = 2,618
Если любое число Фибоначчи, кроме 1 и 2, умножить на четыре и прибавить к определенному числу Фибоначчи, то получится другое число Фибоначчи, так что:
3 × 4 = 12; + 1 = 13
5 × 4 = 20; + 1 = 21
8 × 4 = 32; + 2 = 34
13 × 4 = 52; + 3 = 55
21 × 4 = 84; + 5 = 89
и т. д.
По мере роста новой прогрессии числа образуют третью последовательность, составленную из чисел, прибавленных к произведению четверки и числа Фибоначчи. Это делается возможным в связи с тем, что отношение между членами последовательности, отстоящими друг от друга на две позиции, равно 4,236, где число 0,236 является обратным к 4,236 и, кроме того, разностью между 4,236 и 4. Другие множители приводят к другим последовательностям, все они основаны на коэффициентах Фибоначчи.

