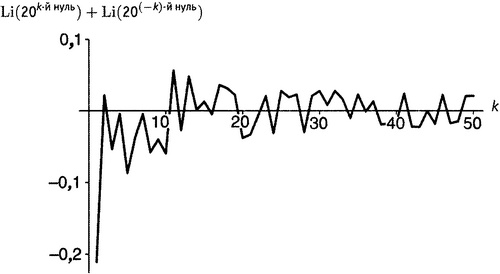
Рисунок 21.5. Первые 50 значений, полученных путем взятия нетривиального нуля и его комплексно сопряженного, вычисления значений функции Li(20z)и их последующего суммирования.
Из рисунка 21.5 видно, почему Риман назвал эти компоненты вторичного члена «периодическими». Они изменяются нерегулярным образом (что означает, если уж быть совсем скрупулезным, что они не строго «периодические», а только «колебательные») вверх и вниз от положительных к отрицательным значениям и обратно.
[200] Причина этого совершенно ясна из рисунка
21.3. Колебательная природа вторичных членов связана с тем, что, как видно из рисунка
21.3, функция Li(xρ) скручивает критическую прямую во все более и более плотную спираль. Значения функции, соответствующие нулям дзета-функции, могут при этом оказаться где угодно на этой спирали; определяющая причина состоит в том, что для больших x критическая прямая чрезвычайно сильно растягивается перед закручиванием. Закручивание настолько плотное, что высоко расположенный отрезок критической прямой отображается в нечто очень близкое по форме к окружности. В силу этого получается, что значения функции Li(xρ) в нулях дзета-функции выглядят примерно как точки, раскиданные по окружности. Если вы немного знакомы с тригонометрией, то вам известно, что это приводит нас в мир синусов и косинусов, волновых функций, колебаний, вибраций… музыки. Именно отсюда и взялось введенное сэром Майклом Берри понятие «музыка простых чисел».
По мере прибавления новых членов сами они убывают, а положительные и отрицательные до некоторой степени сокращают друг друга при суммировании, так что мы зарабатываем сходимость. Эта сходимость, правда, страшно медленная. Для получения результата с точностью в три значащие цифры приходится складывать более 7000 членов; в четыре цифры — более 86 000. На графике на рисунке 21.6 показаны первые 1000 результатов (хотя некоторые из самых левых при выбранном масштабе оказались за пределами рисунка); на этот раз не делается никаких попыток соединить точки между собой. Видно, что члены под знаком суммы действительно уменьшаются, хотя и делают это с достаточной ленцой.
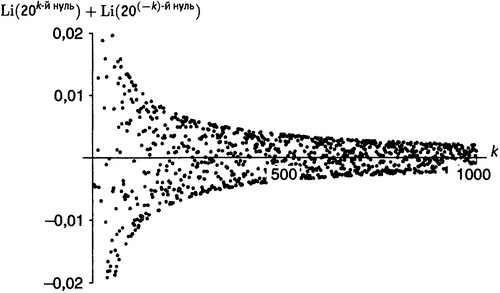
Рисунок 21.6. То же, что на рисунке
21.5, но показана 1000 значений (точки не соединены между собой).
Окончательный результат равен −0,370816425…. Это, как мы помним, второй член в выражении
(21.1). Первый же член — это в нашем случае Li(20), равный 9,90529997763…. Третий равен ln 2, что составляет 0,69314718055994…. И четвертый член, тот самый надоедливый интеграл, добавляет пустячный результат 0,000364111…. Подставим все это в выражение
(21.1) и — хлоп! — J(20) = 9,58333333… (что мы, конечно, и так знали).
VIII.
Закончим тем, что с использованием формулы Римана проведем полное вычисление π(1000 000) — т.е. числа простых чисел в пределах одного миллиона — не ради веселья, хотя веселье и немалое, а для того, чтобы сделать несколько важных замечаний по поводу остаточного члена.
Как мы помним из главы 19.iv,
π(1000 000) = J(1000 000) − 1/2J(√1000 000) − 1/3J(3√1000 000) − ….
Сколько же членов в правой части надо вычислять? До тех пор пока числа в скобках не станут меньше 2, потому что J(x) равна нулю, когда x меньше 2. Корень девятнадцатой степени из 1000 000 равен 2,069138…, а корень двадцатой степени 1,995262… Следовательно, можно остановиться на 19. Поскольку число 19 свободно от квадратов и имеет только один простой делитель — самого себя, — функция Мебиуса μ(19) имеет значение −1. Таким образом, последний член в правой части равен −1/19J(19√1000 000). Всего в правой части будет 13 слагаемых, поскольку между 1 и 19 функция Мебиуса принимает ненулевые значения 13 раз — при аргументах 1, 2, 3, 5, 6, 7, 10, 11, 13, 14, 15, 17, 19. Напомним, что функция Мебиуса равна нулю всякий раз, когда аргумент делится на точный квадрат (например, 4 или 9).
Каждое из этих 13 слагаемых состоит из четырех членов: главный член, вторичный член (куда и входят нули дзета-функции), член с ln 2 и интегральный член. Если сложить все эти 52 куска, получится π(1000 000) — число, про которое мы заранее знаем из главы 3.iii, что оно равно 78 498.
Вся эта арифметика расписана в таблице 21.1 (там опущены строки с N, для которых J(N) равно нулю). Двигаясь вдоль строки N и используя y для обозначения N-го корня из одного миллиона, имеем главный член
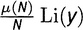 , вторичный член
, вторичный член
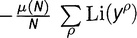 , член с ln 2, равный
, член с ln 2, равный
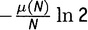 , и интегральный член
, и интегральный член
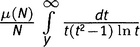 . Суммы по строкам должны быть равны — и в самом деле равны — выражению (μ(N)/N)J(y).
. Суммы по строкам должны быть равны — и в самом деле равны — выражению (μ(N)/N)J(y).
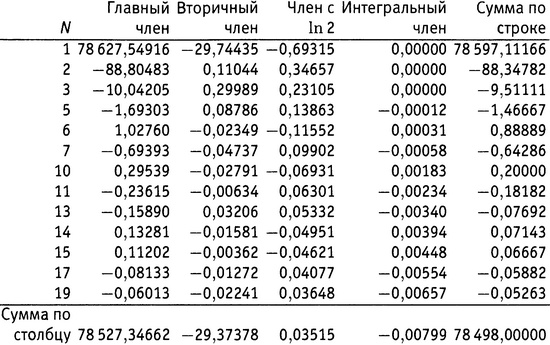
Таблица 21.1. Вычисление π(1000 000).
В качестве простой проверки возьмем строку с N = 6. Поскольку миллион — это 106, корень шестой степени из миллиона — это просто 10. Значение J(10) легко посчитать — оно оказывается равным 16/3. Поскольку число 10 свободно от квадратов и представляет собой произведение двух простых чисел, функция Мебиуса μ(10) имеет значение +1. Итак, в строке с N = 6 последний столбец должен быть равен (+1)×(1/6)×(16/3). Это составляет 8/9, что и говорится в суммарной колонке для строки с N = 6.





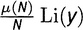 , вторичный член
, вторичный член
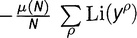 , член с ln 2, равный
, член с ln 2, равный
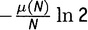 , и интегральный член
, и интегральный член
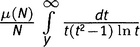 . Суммы по строкам должны быть равны — и в самом деле равны — выражению (μ(N)/N)J(y).
. Суммы по строкам должны быть равны — и в самом деле равны — выражению (μ(N)/N)J(y).