Вскоре вся нация оказалась поглощена конфликтом с Наполеоном, а ее говорящая по-французски аристократия — блеском светской жизни, как это описано Толстым в «Войне и мире». После войны Александр на какое-то время увлекся «управляемым самодержавием», затем последовал провал восстания группировки, боровшейся за либеральные идеи и известной под именем декабристов, и в 1825 году трон перешел к Николаю I, склонному к более старомодному абсолютизму.
Однако подтверждение и возобновление принципов абсолютизма не могло предотвратить грандиозных социальных перемен, наиболее достопамятная из которых — первый великий расцвет русской литературы (Пушкин, Лермонтов и Гоголь). Университет в Санкт-Петербурге, в то время отделенный от академии, разросся и процветал; кроме того, были основаны новые университеты в Москве
[66], Харькове и Казани. Казанский университет мог похвастаться присутствием великого математика Николая Лобачевского, который занимал должность ректора до своего увольнения в 1846 году. Лобачевский был создателем неэвклидовой геометрии, о которой довольно скоро нам будет что сказать.
[67]
В 1849-1850 годах, через 25 лет после воцарения Николая I, интеллектуальная жизнь в России подверглась еще одному всплеску репрессий, вызванному реакцией Николая на европейские революции 1848 года. Число принимавшихся в университеты было сокращено, а учившиеся за границей россияне получили указание вернуться. В такой обстановке молодой преподаватель Санкт-Петербургского университета выпустил две замечательные статьи о ТРПЧ.
Первое, что необходимо сказать о Пафнутии Львовиче Чебышеве, это что его фамилия — кошмар для всякого, кто занимается поиском по базам данных. В своих изысканиях для данной книги я насчитал 32 различных варианта написания его фамилии: Cebysev, Cebyshev, Chebichev, Chebycheff, Chebychev и т.д., и т.д.
[68]
А если вы обратили внимание и на необычное имя Пафнутий, то вы не одиноки. Примерно в 1971 году на него обратил внимание математик Филип Дж. Дэвис. Дэвис решил исследовать происхождение имени Пафнутий и написал о своих изысканиях исключительно забавную книгу «Нить» (1983). Если очень коротко, то имя Пафнутий имеет коптское происхождение (Papnute — «Божий человек») и проникло в Европу через коптское христианство; такое имя носил один из второстепенных Отцов Церкви в IV столетии. Присутствовавший на Никейском соборе епископ Пафнутий (Paphnutius, как обычно пишется его имя) высказывался против целибата духовенства. К более позднему времени относится вскользь упоминаемый Дэвисом преподобный Пафнутий Боровский, сын знатного татарина; в возрасте 20 лет он удалился в монастырь, где и оставался до своей смерти в 94-летнем возрасте (1478). Вот что говорит агиограф этого Пафнутия: «Он был девственник и аскет и в силу этого великий чудотворец и пророк». (Примерно посередине моей работы над этой главой я получил электронное письмо от читательницы моей веб-колонки с просьбой предложить имя для ее новой собаки. Так что теперь некий Пафнутий гоняет белок где-то на Среднем Западе.)
Наш с вами Пафнутий был также в некотором роде чудотворцем. Он удостоился чести добиться единственных реальных успехов на пути к доказательству ТРПЧ в период между тем, как Дирихле поднял Золотой Ключ в 1837 году, и тем, как Риман повернул его в 1859-м. Занятно, что наиболее оригинальная работа Чебышева оказалась в стороне от основного направления исследований по ТРПЧ и послужила образованию менее значительного бокового течения, которое развивалось само по себе и слилось с главным потоком лишь 100 лет спустя.
Чебышев на самом деле написал две статьи по ТРПЧ. Первая, датируемая 1849 годом, озаглавлена «Об определении числа простых чисел, не превосходящих данной величины»
[69]; стоит отметить схожесть с заглавием статьи Римана, написанной 10 лет спустя. В этой работе Чебышев взял Золотой Ключ Эйлера, поиграл с ним немного, примерно как Дирихле за 12 лет до того, и пришел к следующему интересному результату.
Первый результат Чебышева.
Если π(N) ~ CN/ln N для некоторого фиксированного числа C, то C должно быть равным 1.
Вся проблема, конечно, лежала в этом «если». Чебышев не смог преодолеть эту проблему, как, впрочем, в течение полувека не смог и никто другой.
Вторая статья Чебышева, датируемая 1850 годом, значительно более любопытна. Вместо использования Золотого Ключа она начинается с формулы, доказанной шотландским математиком Джеймсом Стирлингом в 1730 году и выражающей приближенные значения факториальной функции для больших чисел. (Факториал числа N равен 1×2×3×4×…×N. Факториал числа 5, например, равен 120: 1×2×3×4×5 = 120. Обычно для факториала числа N используется обозначение N!. Формула Стирлинга утверждает, что для больших значений N его факториал примерно равен
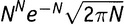 ). Чебышев превратил ее в другую формулу, содержащую ступенчатую функцию — функцию, которая имеет одно значение на некотором интервале аргументов, а затем прыгает к другому значению.
). Чебышев превратил ее в другую формулу, содержащую ступенчатую функцию — функцию, которая имеет одно значение на некотором интервале аргументов, а затем прыгает к другому значению.
Вооруженный только этими средствами и используя ряд вполне элементарных приемов из дифференциального и интегрального исчисления, Чебышев получил два важных результата. Первый состоит в доказательстве «постулата Бертрана», выдвинутого в 1845 году французским математиком Жозефом Бертраном. Постулат гласит, что между любым числом и его удвоением (например, между 42 и 84) всегда найдется простое число. Второй результат Чебышева таков.



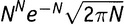 ). Чебышев превратил ее в другую формулу, содержащую ступенчатую функцию — функцию, которая имеет одно значение на некотором интервале аргументов, а затем прыгает к другому значению.
). Чебышев превратил ее в другую формулу, содержащую ступенчатую функцию — функцию, которая имеет одно значение на некотором интервале аргументов, а затем прыгает к другому значению.