И наконец, комплексным сопряжением комплексного числа называется его зеркальное отображение относительно вещественной оси. Комплексное сопряжение числа a + bi есть a − bi. Обозначается оно как z', что произносится как «зет-с-чертой».
{2} Если перемножить комплексное число с его сопряженным, то получится вещественное число: (a + bi)×(a − bi) = a2 + b2, что, как видно, есть квадрат модуля числа a + bi. На этом и основан фокус, позволяющий делить комплексные числа. Используя введенные обозначения, можно записать z×z' = |z|2, а фокус с делением выражается как z/w = (z×w')/|w|2.
Модуль комплексного числа −2,5 + 1,8i, показанного на рисунке
11.2, равен √9,49, то есть около 3,080584, фаза составляет 2,517569 радиана (или, если вам так больше нравится, 144,246113 градуса), а сопряженное число, конечно, есть −2,5 − 1,8i.
VI.
Чтобы продемонстрировать комплексную плоскость в действии, я чуть-чуть потренируюсь в анализе с комплексными числами. Рассмотрим бесконечный ряд из выражения
(9.2):
1/(1 − x) = 1 + x + x2 + x3 + x4 + x5 + x6 + …
(x лежит строго между −1 и 1).
Поскольку здесь не предпринимается никаких действий, кроме сложения, умножения и деления чисел, нет причин, по которым x нельзя было бы сделать комплексным числом. Работает ли эта формула для комплексных чисел? Да, при определенных условиях. Пусть, например, x равен 1/2i. Тогда ряд сходится. Имеем
1/(1 − i/2) = 1 + 1/2i + 1/4i2 + 1/8i3 + 1/16i4 + 1/32i5 + 1/64i6 + …
Левая часть вычисляется с помощью рассмотренного выше фокуса с делением как 0,8 + 0,4i. Правую часть можно упростить, используя тот факт, что i2 = −1:
0,8 + 0,4i = 1 + 1/2i − 1/4 + 1/8i − 1/16 + 1/32i − 1/64 + …
Можно пройти правую часть этой формулы на комплексной плоскости. Идея видна из рисунка
11.3. Начнем из точки 1 (которая, разумеется, расположена на вещественной оси). Оттуда идем на север, что соответствует прибавлению 1/2i. Затем на запад на 1/4 потом на юг в соответствии с вычитанием 1/8i и т.д. Получается спираль, замыкающаяся на комплексном числе 0,8 + 0,4i. Вот вам анализ в действии — бесконечный ряд сходится к этому пределу.
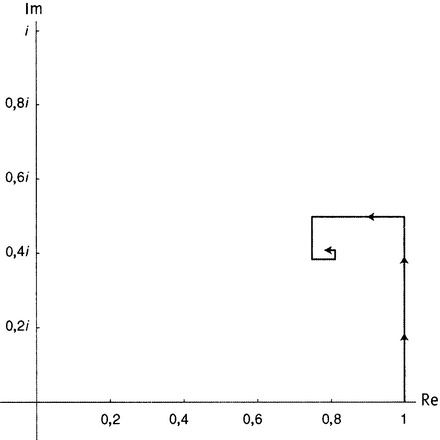
Рисунок 11.3. Анализ на комплексной плоскости.
Заметим, что при переходе к комплексным числам мы потеряли простоту одного измерения, но зато приобрели некоторые преимущества наглядности. При наличии в нашем распоряжении двух измерений можно, как мы только что это и делали, демонстрировать математические результаты в виде замечательных наглядных образов и картинок. В этом до известной степени и состоит привлекательность комплексного анализа (для меня, во всяком случае). В главе 13 мы сможем увидеть дзета-функцию Римана (и саму великую Гипотезу!), выраженную в виде изящных узоров на комплексной плоскости.
Глава 12. Восьмая проблема Гильберта
I.
Давиду Гильберту было 38 лет, когда утром в среду 8 августа 1900 года он выходил к трибуне 2-го международного конгресса математиков. Сын судьи из столицы Восточной Пруссии Кенигсберга
[94], он прославился как математик за 12 лет до того, решив проблему Гордана в теории алгебраических инвариантов.
То был не просто succès d'estime, но до некоторой степени и succès de scandale.
[95] Гильберт смог доказать существование объектов, но при этом не сконструировал их, не предложил даже метода для их построения. Математики говорят о таком как о «доказательстве существования». В своих лекциях Гильберт использовал следующий бытовой пример: «Среди вас имеется по крайней мере один студент — назовем его X, — в отношении которого верно следующее утверждение: ни у одного другого студента в аудитории нет на голове большего числа волос, чем у X. Кто этот студент? Этого мы никогда не узнаем; но в его существовании мы можем быть абсолютно уверены». Доказательства существования довольно распространены в современной математике и в наше время не вызывают особых возражений. Другое дело — Германия 1888 года. Лишь за год до того Леопольд Кронеккер, уважаемый член Берлинской академии наук, выступил с манифестом «О концепции числа», в котором сделал попытку изгнать из математики то, что он считал ненужным уровнем абстракции — все, по его мнению, что нельзя вывести из целых чисел за конечное число шагов. Гордан сам отозвался о гильбертовом доказательстве существования фразой, ставшей знаменитой: «Это не математика. Это теология».
Однако в целом математики признали обоснованность предложенного Гильбертом доказательства. Гильберт вслед за тем продолжил важную работу по алгебраической теории чисел и основаниям геометрии. Он дал новые блестящие доказательства — оба помещающиеся на трех с половиной страницах — трансцендентности чисел π и e. (Когда в 1882 году фон Линдеманн впервые доказал трансцендентность числа π, вышеупомянутый Кронеккер
[96] похвалил его за элегантность доказательства, но добавил, что оно ничего не доказывает, ибо трансцендентные числа не существуют!) В 1895 году Гильберт получил место профессора в Геттингене, где и оставался до своего ухода на пенсию в 1930 году.



