На момент написания книги (середина 2002 года) лучшее достижение принадлежит Картеру Бейсу и Ричарду Хадсону, которые также исходили из теоремы Лемана.
[133] Они показали, что имеются литлвудовы нарушения в окрестности числа 1,39822×10316, а также привели некоторые аргументы в пользу того, что это нарушение может оказаться первым. (Статья Бейса и Хадсона оставляет открытой маленькую лазейку для существования нарушений на более малых высотах, возможно, даже на столь низкой высоте, как 10176. Они также установили существование грандиозной зоны нарушений вблизи числа 1,617×109608.)
VIII.
Колебания остаточного члена Li(x) − π(x) от положительных к отрицательным значениям и затем обратно происходящем не менее в пределах вполне определенных ограничений. Иначе не выполнялась бы ТРПЧ. Некоторые соображения по поводу природы этих ограничений возникли еще в результате усилий, направленных на доказательство ТРПЧ. Де ля Валле Пуссен включил в свое доказательство ТРПЧ некоторую оценку для функции, выражающей это ограничение. Пять лет спустя шведский математик Хельге фон Кох
[134] доказал следующий ключевой результат, который я сформулирую в его современной записи.
Результат фон Коха 1901 года
Если Гипотеза Римана верна, то
π(x) = Li(x) + Ο(√x∙ln x).
Уравнение здесь читается так: «Пи от икс равно интегральному логарифму от икс плюс Ο большое от корня из икс, умноженного на логарифм икс». Теперь надо объяснить, что же такое «О большое».
{3}
Глава 15. О большое и мебиусово мю
I.
Эта глава посвящена двум математическим темам, которые связаны с Гипотезой Римана, но помимо этого друг с другом никак не связаны. Эти темы — «Ο большое» и мю-функция Мебиуса. Рассмотрим сначала Ο большое.
II.
Когда Пауль Туран — великий венгерский математик, занимавшийся теорией чисел, — умирал от рака в 1976 году, его жена находилась у его постели. Она сообщила, что его последние слова были «Ο большое от единицы». Математики передают эту историю с благоговением: «Заниматься теорией чисел до самого конца! Истинный математик!»
Ο большое пришло в математику из книги Ландау 1909 года, влияние которой, как я уже рассказывал, было поистине огромным. Ландау на самом деле не изобрел Ο большое. Он чистосердечно признается на странице 883 своего Handbuch, что позаимствовал его из трактата Пауля Бахманна 1894 года. Поэтому довольно несправедливо называть его «ландаувским О большим» равно как несправедливо и то, что многие математики, по-видимому, полагают, что именно Ландау его изобрел. Ο большое присутствует повсеместно в аналитической теории чисел и даже просочилось оттуда в другие области математики.
Ο большое — это способ наложить ограничение на величину функции, когда аргумент устремляется к (как правило) бесконечности.
Определение Ο большого
Функция A есть Ο большое от функции B, если для достаточно больших аргументов величина A никогда не превосходит некоторого фиксированного кратного величины B.
Вслед за Паулем Тураном рассмотрим Ο большое от единицы. «Единица» здесь понимается как функция, причем функция простейшего вида. Ее график — горизонтальная прямая, проходящая на высоте 1 над горизонтальной осью. Для вообще любых аргументов значение этой функции равно… просто 1. Ну и что же тогда означает, что функция f(x) есть Ο большое от единицы? По только что данному определению это означает, что, когда аргумент x уходит на бесконечность, f(x) никогда не превзойдет некоторого фиксированного кратного 1 — другими словами, график функции f(x) навсегда останется ниже некоторой горизонтальной прямой. Это полезная информация о данной нам функции f(x). Существует множество функций, для которых это не так. Это не так, например, для x2 и для x в любой положительной степени, ни для ex ни даже для ln x.
На самом деле Ο большое означает еще кое-что, кроме этого. Заметим, что в определении сказано «величина A». Это означает «значение A без учета знака». Величина числа 100 есть 100; величина числа −100 есть также 100. Ο большое не принимает в расчет знак минус. Сказать, что некоторая функция f(x) есть Ο большое от единицы, означает сказать, что f(x) навсегда заключена между двумя горизонтальными прямыми, одна из которых проходит выше горизонтальной оси, а другая проходит на таком же расстоянии ниже.
Как уже говорилось, очень многие функции не являются Ο большим от единицы. Простейшая из них — это функция x, то есть функция, значения которой всегда равны ее аргументу. Ее график — диагональная прямая, покидающая рисунок в верхнем правом углу. Ясно, что она не заключена между какими бы то ни было горизонтальными прямыми. Вне зависимости оттого, сколь широко вы расположите эти горизонтальные прямые, функциях рано или поздно вырвется за их пределы. Это останется верным, если уменьшить наклон. Функции 0,1x (показана на рисунке 15.1), 0,01x, 0,001x и 0,0001x все в конце концов прорвутся через любые горизонтальные прямые, которые вы установите в качестве ограничения. Ни одна из них не является Ο большим от единицы.
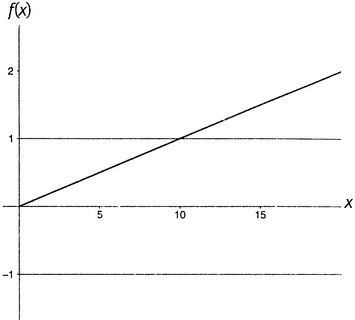
Рисунок 15.1. Функция 0,1x не есть Ο большое от единицы.



