Первый член в бесконечной сумме: берем 1 из каждой скобки. Это даст бесконечное произведение 1×1×1×1×1×…, значение которого есть, конечно, просто 1.
Второй член: берем 1 из всех скобок, кроме первой. Из первой же возьмем
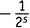 . Это даст бесконечное произведение
. Это даст бесконечное произведение
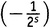 ×1×1×1×1×…, которое равно просто
×1×1×1×1×…, которое равно просто
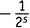 .
.
Третий член: берем 1 из каждой скобки, кроме второй. А из второй возьмем
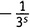 . Это даст бесконечное произведение 1×
. Это даст бесконечное произведение 1×
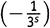 ×1×1×1×…, что равно просто
×1×1×1×…, что равно просто
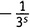 .
.
Четвертый член… Я думаю, понятно, что, если брать 1 из каждой скобки, кроме n-й, мы получим слагаемое равное
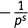 , где p — n-е простое число. Итак, получилась бесконечная сумма вида (15.3):
, где p — n-е простое число. Итак, получилась бесконечная сумма вида (15.3):
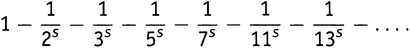
Но это еще не конец. При перемножении скобок возникает сумма всех возможных членов, получаемых взятием одного числа из каждой скобки. Предположим, мы выбрали
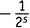 из первой скобки,
из первой скобки,
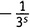 из второй и 1 из всех остальных. Это дает
из второй и 1 из всех остальных. Это дает
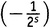 ×
×
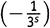 ×1×1×1×…, что равно
×1×1×1×…, что равно
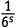 . Похожие вещи мы получим из каждой возможной пары выборов не-единиц. Выбирая из третьей скобки
. Похожие вещи мы получим из каждой возможной пары выборов не-единиц. Выбирая из третьей скобки
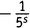 и
и
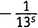 из шестой, а единицы из всех остальных, получаем член, равный
из шестой, а единицы из всех остальных, получаем член, равный
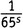 .
.
(Заметим, что здесь работают два простых правила арифметики. Одно — это правило знаков, гласящее, что минус умножить на минус дает плюс, а другое — 7-е правило действий со степенями, согласно которому (x×y)n = xn×yn.)
Так что наряду с членами, уже собранными в выражении
(15.3), имеется новый набор, каждый член в котором происходит из каждой пары простых чисел, как 5 и 13, и которые все входят со знаком плюс. Таким образом, выражение
(15.3) разрослось до такого:
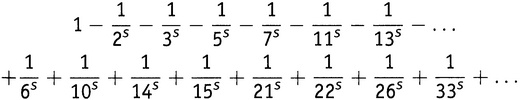
где каждое число во второй строке есть произведение двух различных простых.
А ведь мы едва начали нашу деятельность по перемножению бесконечного числа скобок. Следующий шаг состоит в том, чтобы перебрать все возможные способы выбрать три не-единицы (при всех остальных единицах). Например, 1×
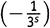 ×1×1×
×1×1×
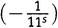 ×
×
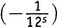 ×1×1×…, из чего возникает
×1×1×…, из чего возникает
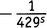 .Теперь результат разрастается до
.Теперь результат разрастается до



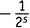 . Это даст бесконечное произведение
. Это даст бесконечное произведение
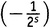 ×1×1×1×1×…, которое равно просто
×1×1×1×1×…, которое равно просто
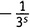 . Это даст бесконечное произведение 1×
. Это даст бесконечное произведение 1×
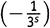 ×1×1×1×…, что равно просто
×1×1×1×…, что равно просто
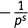 , где p — n-е простое число. Итак, получилась бесконечная сумма вида (15.3):
, где p — n-е простое число. Итак, получилась бесконечная сумма вида (15.3):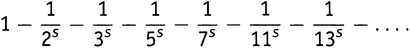
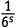 . Похожие вещи мы получим из каждой возможной пары выборов не-единиц. Выбирая из третьей скобки
. Похожие вещи мы получим из каждой возможной пары выборов не-единиц. Выбирая из третьей скобки
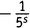 и
и
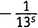 из шестой, а единицы из всех остальных, получаем член, равный
из шестой, а единицы из всех остальных, получаем член, равный
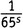 .
.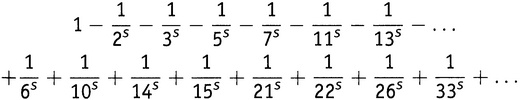
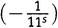 ×
×
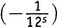 ×1×1×…, из чего возникает
×1×1×…, из чего возникает
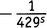 .Теперь результат разрастается до
.Теперь результат разрастается до