Теперь можно, наконец, продемонстрировать график функции π(x) (рис. 19.1). К ступенчатым функциям не сразу привыкаешь, но с математической точки зрения они представляют собой совершенно нормальное явление. Область определения у нас сейчас — все неотрицательные числа. В этой области определения для каждого аргумента имеется единственное значение нашей функции. Дайте мне аргумент, и я скажу вам значение. В математике бывают функции и покруче.
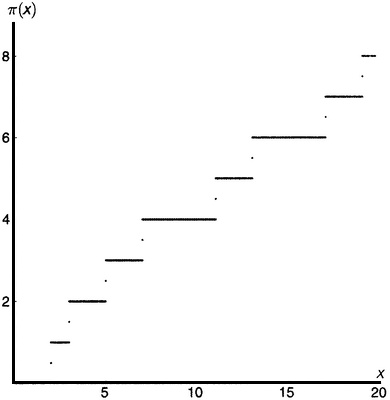
Рисунок 19.1. Функция, считающая простые числа.
III.
Теперь введем другую функцию — также ступенчатую, но при этом слегка более хитрую, чем π(x). В статье 1859 года Риман называет ее просто «функция f», но мы вслед за Хэролдом Эдвардсом будем называть ее «функцией J». Со времен Римана математики привыкли использовать f для обозначения функции вообще: «Пусть f — произвольная функция…» — так что они могут слегка напрячься, увидев f в роли некоторой конкретной функции.
Итак, определим функцию J. Для любого неотрицательного числа x значение функции J равно
J(x) = π(x) + 1/2π(√x) + 1/3π(3√x) + 1/4π(4√x) + 1/5π(5√x) + …. (19.1)
Здесь «π» обозначает функцию числа простых чисел именно в том виде, как выше мы ее определили для любого вещественного числа x.
Заметим, что приведенная сумма — не бесконечная. Чтобы убедиться в этом, возьмем любое фиксированное число x, скажем, x = 100. Квадратный корень из 100 равен 10; кубический корень равен 4,641588…; корень четвертой степени равен 3,162277…; корень пятой степени 2,511886…; корень шестой степени 2,154434…; корень седьмой степени 1,930697…; корень восьмой степени 1,778279…; корень девятой степени 1,668100… и корень десятой степени равен 1,584893…. Можно было бы, конечно, вычислить и корни одиннадцатой, двенадцатой, тринадцатой степени и т.д., сколько вам заблагорассудится, но в этом нет необходимости, потому что функция числа простых чисел обладает таким очень приятным свойством: если x меньше 2, то π(x) равна нулю — просто потому, что нет никаких простых чисел, меньших 2! Таким образом, при вычислении корней из 100 можно было на самом деле остановиться после корня седьмой степени. Вот что мы в результате имеем:
J(100) = π(100) + 1/2π(10) + 1/3π(4,64…) + 1/4π(3,16…) + 1/5π(2,51…) + 1/6π(2,15…) + 0 + 0 + …,
и если теперь сосчитать число простых, то это равно
J(100) = 25 + (1/2×4) + (1/3×2) + (1/4×2) + (1/5×1) + (1/6×1),
что дает 288/15 или 28,53333…. При извлечении корней из любого числа рано или поздно значения падают ниже 2, и начиная с этого места все члены в выражении для функции J равны нулю. Поэтому для любого аргумента x значение функции J(x) можно получить, вычисляя конечную сумму — существенное улучшение по сравнению с некоторыми из функций, что нам встречались!
Как уже говорилось, функция J ступенчатая. На рисунке 19.2 показано, как она выглядит при аргументах до 10. Как видно, функция J совершает прыжок от одного значения к другому, остается на новом значении на некоторое время, потом совершает новый прыжок. Что это за прыжки? Какой закон за ними стоит?
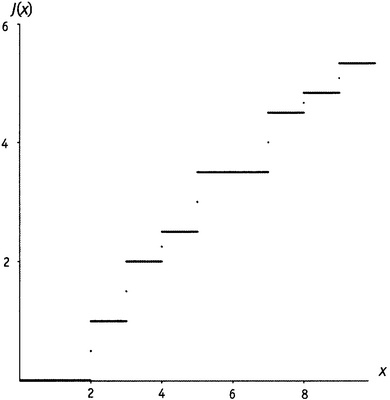
Рисунок 19.2. Функция J(x).
Вглядевшись очень внимательно в выражение
(19.1), мы увидим следующую закономерность. Во-первых, когда x — простое число, функция J(x) совершает прыжок на высоту 1, потому что π(x) — число простых чисел, не превышающих x, — при этом увеличивается на 1. Во-вторых, когда x является точным квадратом простого числа (например, x = 9, что есть квадрат числа 3), J(x) совершает прыжок на одну вторую, потому что квадратный корень из x есть простое число, а значит, π(√x) возрастает на 1. В-третьих, когда x есть точный куб простого числа (например, x = 8, что есть куб числа 2), J(x) совершает прыжок на одну треть, потому что кубичный корень из x равен простому числу, а значит, π(3√x) возрастает на 1, и т.д.
Попутно заметим, что функция J обладает тем же свойством, которым мы снабдили функцию π(x): в точке, где реально происходит прыжок, она принимает значение, лежащее посередине между теми значениями, от которого и до которого она прыгает.
Для полноты представления функции J на рисунке 19.3 изображен график J(x) при аргументах до 100. Самый маленький прыжок здесь совершается при x = 64 — это число представляет собой шестую степень (64 = 26), так что функция J прыгает при x = 64 на одну шестую.
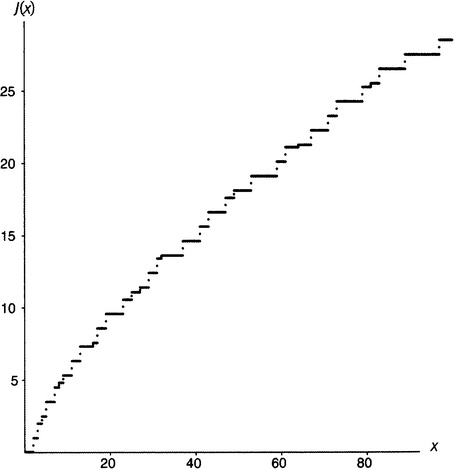
Рисунок 19.3. Еще о функции J(x).
Какую пользу может принести подобная функция? Терпение, терпение. Сначала придется совершить один из тех логических скачков, о которых я предупреждал в начале главы.
IV.
Напоминаю в который уже раз, что у математиков есть масса способов обращать соотношения. Дали нам выражение для P через Q — отлично, посмотрим, не найдется ли способа выразить Q через P. В течение столетий в математике был развит целый инструментарий для того, чтобы совершать обращения, — он включает набор приемов для использования в самых разных условиях и обстоятельствах. Один из таких приемов носит название мебиусова обращения, и оно-то нам сейчас и нужно.
Не буду пытаться объяснить мебиусово обращение в общем виде. Оно описано в любом хорошем учебнике по теории чисел (см., например, раздел 16.4 в классической монографии «Теория чисел» Харди и Райта), а кроме того, поиск в Интернете наведет вас на множество ссылок. Подражая до некоторой степени самим функциям π и J, я вместо того, чтобы уныло тащиться от одной точки в моих рассуждениях к другой, перескочу сразу к следующему факту: применение мебиусова обращения к выражению
(19.1) дает такой результат:





