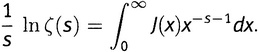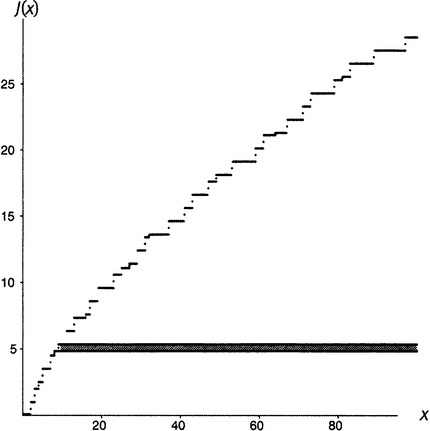
Рисунок 19.4.
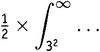 .
.
Конечно, площадь под графиком функции J бесконечна. Нарисованная полоска уже имеет бесконечную площадь (высота 1/2, длина бесконечна, площадь 1/2×∞ = ∞). Таковы же площади и всех других полосок. Все вместе они складываются в бесконечность. Но что, если я пожелаю «придавить» функцию J справа таким образом, чтобы площадь под графиком стала конечной? Так, чтобы каждая из этих полосок постепенно сужалась и сжималась до такой степени, чтобы площадь ее стала конечной? Как можно было бы осуществить такое «придавливание»?
Последний интеграл подсказывает как. Предположим, что мы взяли какое-нибудь число s (которое будем считать большим единицы). Для каждого аргумента x умножим J(x) на x−s−1. Для иллюстрации возьмем s = 1,2. Тогда x−s−1 = x−2,2 или, другими словами, 1/x2,2. Возьмем аргумент x, скажем, равным 15. Вот, J(15) есть 7,333333…, а 15−2,2 равно 0,00258582…. Перемножая, получаем, что J(x)x−s−1 имеет значение 0,018962721…. Если брать большие аргументы, то сдавливание будет выражено более ярко. При x = 100 значение выражения J(x)x−s−1 равно 0,001135932….
На рисунке 19.5 показан график функции J(x)x−s−1 при s = 1,2. Чтобы подчеркнуть «эффект сдавливания», там показана та же самая полоска, которая была выделена и ранее, но теперь после сдавливания. Видно, как она все более и более худеет по мере того, как аргумент устремляется на восток. Имеется вполне реальный шанс, что вся площадь окажется конечной, несмотря на свою бесконечную длину. В предположении, что так и есть и что дело обстоит таким же образом для всех полосок, спросим себя: какова же будет полная площадь под графиком этой функции? Или, выражаясь математически, каково будет значение
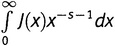 ?
?
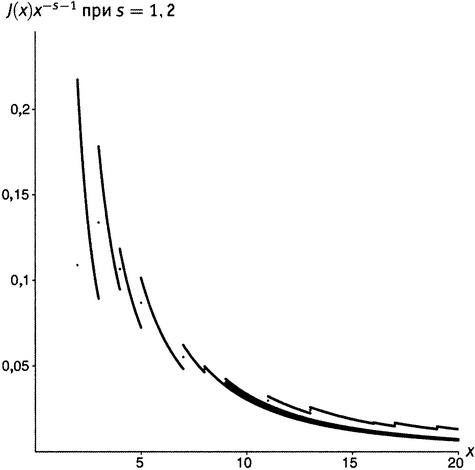
Рисунок 19.5.
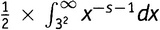 при s = 1,2.
при s = 1,2.
Давайте посмотрим. Будем перебирать простые числа одно за одним. Для простого числа 2 до сдавливания имеем полоску высоты 1, идущую от 2 до бесконечности, далее полоску высоты идущую от 22 до бесконечности, затем полоску высоты идущую от 23 до бесконечности, и т.д. Сумма площадей сдавленных полосок — если мы рассматриваем пока только простое число 2 — равна (19.4):
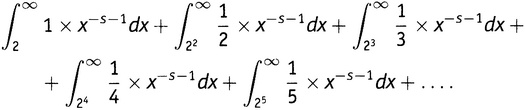
Конечно, это пока только 2-полоски. Имеется аналогичная бесконечная сумма интегралов для 3-полосок (19.5):
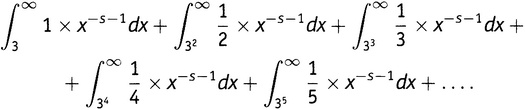
И аналогичная сумма для 5, потом для 7 и т.д. для всех простых чисел. Бесконечная сумма бесконечных сумм интегралов! Все хуже и хуже! Да, но самый густой мрак перед рассветом.
Это возвращает нас к началу данного раздела. Поскольку интеграл прозрачен для умножения на число,
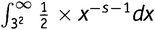 — это то же самое, что
— это то же самое, что
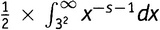 . Но в начале раздела мы видели, что член, который мы в качестве пробного выбрали в выражении
(19.3), т.е.
. Но в начале раздела мы видели, что член, который мы в качестве пробного выбрали в выражении
(19.3), т.е.
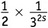 , равен
, равен
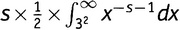 — другими словами, s умножить на то, что мы только что получили. Так к чему же сводится выражение
(19.5)? Вот именно, в точности ко второй строке в выражении
(19.3), деленной на s! А выражение
(19.4) плюс выражение
(19.5) плюс аналогичные выражения для всех остальных простых чисел суммируются к выражению
(19.3), деленному на s. Вот и рассвет! Получается, что штука, с которой я тут забавляюсь, т.е.
— другими словами, s умножить на то, что мы только что получили. Так к чему же сводится выражение
(19.5)? Вот именно, в точности ко второй строке в выражении
(19.3), деленной на s! А выражение
(19.4) плюс выражение
(19.5) плюс аналогичные выражения для всех остальных простых чисел суммируются к выражению
(19.3), деленному на s. Вот и рассвет! Получается, что штука, с которой я тут забавляюсь, т.е.
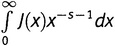 , равна просто выражению
(19.3), деленному на s. Но выражение
(19.3) равно ln ζ(z), как нам подсказывает Золотой Ключ. Отсюда получается следующий результат.
, равна просто выражению
(19.3), деленному на s. Но выражение
(19.3) равно ln ζ(z), как нам подсказывает Золотой Ключ. Отсюда получается следующий результат.
Золотой Ключ (аналитический вариант) (19.6)
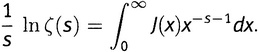
Я просто не нахожу слов, чтобы выразить, насколько это чудесный результат. Он ведет прямо к центральному результату в работе Римана — результату, который будет предъявлен в главе 21. На самом деле это просто переписывание Золотого Ключа в терминах анализа. Однако переписать его так — это невероятно мощное достижение, потому что теперь Золотой Ключ открыт для всех мощных средств дифференциального и интегрального исчисления XIX века. В этом состояло достижение Римана.


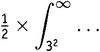 .
.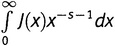 ?
?
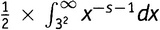 при s = 1,2.
при s = 1,2.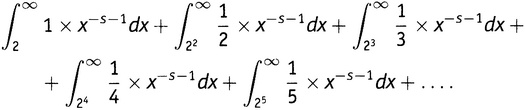
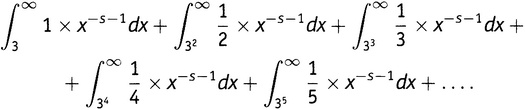
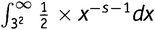 — это то же самое, что
— это то же самое, что
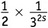 , равен
, равен
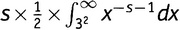 — другими словами, s умножить на то, что мы только что получили. Так к чему же сводится выражение
(19.5)? Вот именно, в точности ко второй строке в выражении
(19.3), деленной на s! А выражение
(19.4) плюс выражение
(19.5) плюс аналогичные выражения для всех остальных простых чисел суммируются к выражению
(19.3), деленному на s. Вот и рассвет! Получается, что штука, с которой я тут забавляюсь, т.е.
— другими словами, s умножить на то, что мы только что получили. Так к чему же сводится выражение
(19.5)? Вот именно, в точности ко второй строке в выражении
(19.3), деленной на s! А выражение
(19.4) плюс выражение
(19.5) плюс аналогичные выражения для всех остальных простых чисел суммируются к выражению
(19.3), деленному на s. Вот и рассвет! Получается, что штука, с которой я тут забавляюсь, т.е.