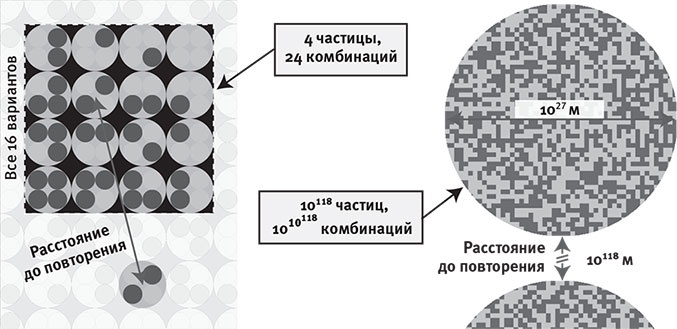
Рис. 6.2. В игрушечной вселенной, где в 4 местах может находиться по одной частице двух типов, существует всего 24 возможных комбинаций (вверху слева). Это означает, что в мультиверсе I типа, состоящем из таких вселенных, в среднем нужно проверить 16 вселенных, чтобы найти повторение одной заданной. Если наша Вселенная подобным же образом содержит 10118 частиц, которые можно скомбинировать 1010 118 различными способами, придётся посетить около 1010 118 параллельных вселенных, прежде чем отыщется идентичная копия.
Хотя число 1010 118 настолько велико, что его не назовёшь даже астрономическим, оно ничтожно в сравнении с бесконечностью. Это означает, что если вечная инфляция породила пространство, содержащее бесконечно много параллельных вселенных I уровня, среди них найдутся все возможные варианты. В частности, вам придётся проверить в среднем около 1010 118 вселенных, прежде чем вы найдёте копию любой вселенной (рис. 6.2). Так что если вы станете путешествовать по прямой линии, пока не наткнётесь на ближайшую копию нашей Вселенной, то пройденный вами путь составит примерно 1010 118 диаметров Вселенной. Если же вы станете искать во всех направлениях, то расстояние до ближайшей нашей копии выразится примерно тем же числом, и это будет примерно то же самое, что 1010 118 м — таково забавное математическое поведение двойных степеней (степеней в показателях степени).
[25]
Существенно ближе, на расстоянии около 101091 м, должна найтись сфера радиусом 100 световых лет, идентичная сфере с центром на Земле, где всё, что мы будем воспринимать в течение ближайшего столетия, окажется идентичным тому, что воспринимают там наши двойники. Примерно в 101029 м от нас должна найтись ваша идентичная копия. На самом деле, ваши копии, по-видимому, должны быть гораздо ближе, поскольку процессы образования планет и биологической эволюции, итог которых оказался в вашу пользу, везде одинаковы. В объёме одной лишь нашей Вселенной должно быть не менее 1020 планет.
Мультиверс II уровня
Помните, я назвал теорию инфляции благодатным даром? Когда начинает казаться, что она не может предсказать что-либо более радикальное, чем уже предсказано, ей это удаётся. Если вам было трудно переварить огромный мультиверс I уровня, попробуйте представить себе бесконечное множество таких мультиверсов, причём в некоторых могут действовать совершенно иные законы физики. Андрей Линде, Александр Виленкин, Алан Гут и их коллеги показали, что именно это обычно предсказывает теория инфляции. (А мы будем называть это мультиверсом II уровня.)
Много вселенных в одном пространстве
Как вообще физика может позволять такое безумие? Вспомните (рис. 5.8), что инфляция умудряется породить бесконечный объём внутри конечного. На рис. 6.3 показано, что нет причин, согласно которым инфляция не могла бы осуществить это в нескольких примыкающих друг к другу объёмах. В результате получилось бы несколько бесконечных областей (мультиверсов I уровня) — при условии, что инфляция вечна и никогда не заканчивается на границах между этими объёмами. Это означает, что если вы живёте в одном из мультиверсов I уровня, посещение соседнего невозможно: инфляция продолжает порождать разделяющее вас пространство быстрее, чем вы можете его преодолевать. Я представил, как разговариваю с детьми, расположившимися на заднем сиденье моей ракеты:
— Папа, мы уже приехали?
— Нам остался один световой год.
— Папа, мы уже приехали?
— Нам осталось два световых года.
Иными словами, хотя эти другие части мультиверса II уровня находятся в том же пространстве, что и мы, они более чем бесконечно далеки от нас в том смысле, что мы никогда их не достигнем, даже если будем вечно путешествовать со скоростью света. Напротив, сколь угодно отдалённых частей нашего мультиверса I уровня, в принципе, можно достичь, если у вас хватит терпения и если космологическое расширение замедляется.
[26]
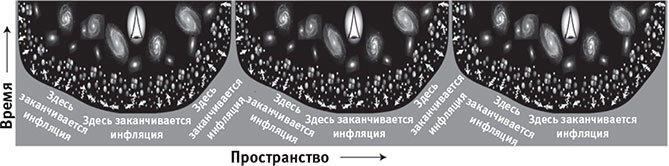
Рис. 6.3. Если вечная инфляция порождает три бесконечные области посредством механизма, изображённого на рис. 5.8, то путешествовать между ними невозможно, поскольку инфляция порождает пространство между вами и местом назначения быстрее, чем вы можете его преодолевать.
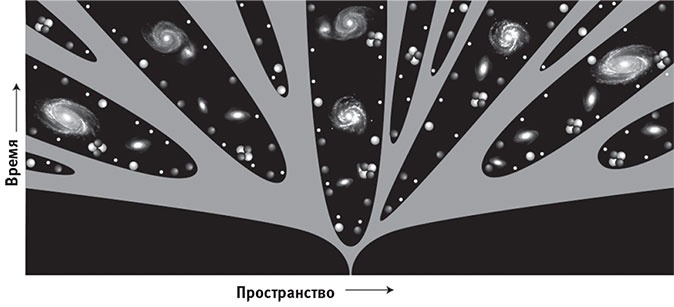
На рис. 6.3 я сделал упрощение, проигнорировав тот факт, что пространство расширяется. Вечно инфлирующие области я обозначил тонкими вертикальными полосками, разделяющими U-образные мультиверсы I уровня. В действительности они будут быстро расширяться и в конце концов инфляция в части пространства внутри них прекратится, породив дополнительные U-образные области. Так ещё интереснее: мультиверс II уровня оказывается древоподобной структурой (рис. 6.4). Любая инфлирующая область продолжает быстро расширяться, но инфляция рано или поздно в различных её частях заканчивается, порождая U-образные области, и каждая из них представляет собой бесконечный мультиверс I уровня. Это древо продолжает расти вечно, создавая бесконечное число таких U-образных областей, и все они вместе образуют мультиверс II уровня. Завершение инфляции превращает инфлирующую субстанцию внутри каждой области в частицы, которые затем собираются в атомы, звёзды и галактики. Алан Гут любит называть мультиверсы I уровня «карманными вселенными», поскольку они аккуратно заполняют небольшие участки «кроны» древа.





