Если при решении математической задачи вы оказались в тупике, последуйте совету Пуанкаре: отвлекитесь и займитесь чем-нибудь другим. Если вам повезет и ветер будет попутным, у вас рано или поздно появится новая идея. Специалисты по теории чисел вряд ли осознанно следовали этому совету, но тем не менее они поступали именно так. Как и утверждал Пуанкаре, такая тактика срабатывала. Некоторые специалисты по теории чисел перенесли внимание на эллиптические кривые (см. главу 6). По иронии судьбы, со временем именно в этой области математики выявились поразительные и неожиданные связи с Великой теоремой Ферма, которые и привели, в конце концов, к доказательству Уайлса. Для описания этих связей нам потребуется еще одно понятие — модулярной функции. С этого момента наше обсуждение приобретет несколько технический характер, но за всем этим стоит вполне разумная история, да нам и нужны-то лишь самые общие положения. Следите за моими рассуждениями.
В главе 6 мы видели, что теория эллиптических функций сильно повлияла на развитие комплексного анализа. В 1830-е гг. Жозеф Лиувилль открыл, что разновидностей эллиптических функций не так уж много. Для любых двух периодов существует особая эллиптическая функция, известная как функция Вейерштрасса, и любая другая эллиптическая функция с теми же двумя периодами является просто ее вариантом. Тем самым подразумевается, что из функций с двойной периодичностью достаточно разобраться в функциях Вейерштрасса — по одной на каждую пару периодов.
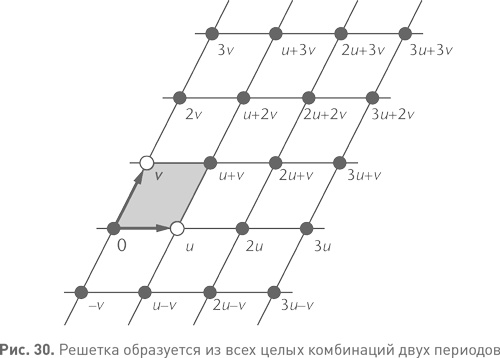
Геометрически двойную периодическую структуру эллиптической функции можно интерпретировать как решетку на комплексной плоскости: это все комбинации вида mu + nv двух периодов u и v (см. рис. 30). Если мы возьмем комплексное число z и добавим к нему одну из точек нашей решетки, то значение эллиптической функции в новой точке будет тем же, что и в первоначальной. Иными словами, эллиптическая функция обладает той же симметрией, что и описанная решетка.
Аналитики открыли гораздо более богатый источник симметрий комплексной плоскости, известный как преобразования Мёбиуса. Эти преобразования превращают z в (az + b)/(cz + d), где a, b, c, d — комплексные константы. Симметрии, определяемые решеткой, представляют собой особые случаи преобразований Мёбиуса, но существуют и другие. Однако в более общем случае тоже присутствует набор точек, аналогичный рассмотренной нами решетке. Решетка определяет на евклидовой плоскости ячеистую структуру: достаточно взять в виде ячейки параллелограмм и поместить его углы в узлы решетки (см. рис. 26 и 30). При помощи преобразований Мёбиуса мы можем построить ячеистую структуру в подходящей неевклидовой геометрии, на гиперболической поверхности. Мы можем установить тождественность этой поверхности и части комплексной плоскости, где прямые заменяются дугами окружностей.
В гиперболической геометрии существуют весьма симметричные ячеистые структуры. Для каждой из них можно построить комплексные функции, которые на каждой ячейке повторяют свои значения. Такие функции известны как модулярные и представляют собой естественное обобщение эллиптических функций. Гиперболическая геометрия — очень насыщенная область математики, и диапазон ячеистых структур здесь намного шире, чем на евклидовой плоскости. Поэтому специалисты по комплексному анализу всерьез заинтересовались неевклидовой геометрией. При этом выявилась глубокая связь между математическим анализом и теорией чисел. Модулярные функции играют для эллиптических кривых ту же роль, что тригонометрические функции для окружности.
Напомню, что единичная окружность состоит из точек (x, y), таких, что x² + y² = 1. Пусть A — действительное число, и
Тогда определение синуса и косинуса говорит о том, что данная точка лежит на единичной окружности. Более того, любая точка единичной окружности имеет такую форму. Говоря математическим языком, эти тригонометрические функции представляют окружность в параметрическом виде. Что-то очень похожее происходит и с модулярными функциями. Если мы определим x и y при помощи подходящих модулярных функций параметра A, то соответствующая точка будет лежать на эллиптической кривой — одной и той же эллиптической кривой, какое бы значение ни принимал параметр A. Существуют и более абстрактные способы сформулировать вышеизложенное, и специалисты пользуются именно ими, потому что они удобнее, но этот вариант позволяет выявить аналогию с тригонометрическими функциями и окружностью. Эта связь порождает свою эллиптическую кривую для каждой модулярной функции, а разнообразие модулярных функций громадно — ведь это все симметричные ячеистые структуры на гиперболической поверхности. Итак, огромное количество эллиптических кривых может быть соотнесено с модулярными функциями. Но какие эллиптические кривые можно получить таким способом? Именно этот вопрос оказался главным.
Впервые это «недостающее звено» привлекло внимание ученых в 1975 г., когда Ив Эллегуар обратил внимание на занятную связь между Великой теоремой Ферма и эллиптическими кривыми. Герхард Фрей в двух статьях, опубликованных в 1982 и 1986 гг., развил эту идею. Пусть p, как всегда, нечетное простое число. Предположим — в надежде прийти к противоречию, — что существуют ненулевые целые числа a, b и c, удовлетворяющие уравнению Ферма, так что ap + bp = cp. А теперь с надлежащей помпой извлечем из шляпы заранее припасенного кролика: рассмотрим эллиптическую кривую
y² = x (x — ap) (x — bp).
Эта кривая называется эллиптической кривой Фрея. Фрей применил к ней механизм работы с эллиптическими кривыми и получил цепочку еще более причудливых совпадений. Его гипотетическая эллиптическая кривая выглядит и правда очень странно. На первый взгляд, она вообще лишена смысла. Фрей доказал, что смысла в ней настолько мало, что она не может существовать. И это обеспечивает нам желанное противоречие и тем самым, разумеется, доказывает Великую теорему Ферма.
Однако в этом доказательстве есть пробел, и Фрей прекрасно знал о нем. Чтобы доказать, что такая эллиптическая кривая не существует, необходимо показать, что если бы она существовала, то была бы модулярной, т. е. одной из тех кривых, что возникают из модулярных функций. Мы только что убедились, что таких кривых множество; на тот момент никому не удавалось отыскать хотя бы одну эллиптическую кривую, которая не была бы модулярной. Казалось логичным, что и кривая Фрея должна быть модулярной, но это была гипотетическая кривая, коэффициенты a, b и c не были известны. К тому же, если бы кривая и правда была модулярной, то она просто не могла бы существовать. Был, однако, один способ раз и навсегда разобраться со всеми этими вопросами: доказать, что все эллиптические кривые модулярны. Тогда кривая Фрея, гипотетическая или нет, тоже была бы модулярной, если бы существовала. А если бы ее не было, то доказательство от этого никак бы не пострадало.