Хотя Шимура был не чужд некоторых причуд (он и поныне питает слабость к анекдотам о мудрецах, проповедующих дзен-буддизм), он был более консервативен и традиционен, чем его коллега. Шимура поднимался на рассвете и сразу же приступал к работе. Танияма же частенько не ложился спать, проработав всю ночь напролет. Те, кто заглядывал днем к нему в номер, нередко заставали его спящим.
Шимура был скрупулезен и строг, Танияма небрежен, почти ленив. Удивительно, но именно эта черта в Танияме особенно импонировала Шимуре: «Он обладал особым даром совершать множество ошибок, в основном в правильном направлении. Я завидовал этой его особенности и даже пытался подражать ему, но обнаружил, что совершать хорошие ошибки очень трудно».
Танияма был живым воплощением рассеянного гения, и это отражалось и на его внешности. Он был неспособен крепко завязать шнурки на ботинках и поэтому решил вместо того, чтобы по десять раз на день делать одно и тоже, вообще их не завязывать. Он всегда носил один и тот же весьма приметный зеленый костюм с металлическим отливом. Костюм был сшит из ткани, настолько кричащей, что остальные члены семьи отказались от нее.
Когда Танияма и Шимура встретились в 1954 году, они оба были начинающими математиками. По традиции, существующей и до сих пор, молодых аспирантов берет «под крыло» профессор, руководящий их становлением как математиков. Танияма и Шимура отвергли такую форму ученичества. Во время войны настоящие математические исследования прекратились, и даже к 50-м годам математический факультет еще не возродился. По словам Шимуры, профессора были «усталы, измучены и разочарованы». Что же касается послевоенных студентов и аспирантов, то они были преисполнены энергии и страстно хотели учиться. Вскоре аспиранты поняли, что единственный доступный им способ изучать математику заключается в том, чтобы обучать друг друга. Они организовали регулярно действующие семинары, на которых по очереди информировали друг друга о новейших идеях, результатах и методах. Несмотря на свою вялость и апатичность, Танияма, когда речь заходила о семинарах, преисполнялся всесокрушающей энергией. Аспирантов постарше он поощрял к тому, чтобы те смелее вторгались на еще неизведанную территорию, а по отношению к аспирантам младше себя и студентам выступал в роли учителя. Научная изоляция Японии привела к тому, что эти семинары занимались задачами, которые, как правило, в Европе и Америке считалась давно пройденными. Одна вышедшая из моды тема, а именно, исследование модулярных форм, казалась особенно привлекательной Танияме и Шимуре, Модулярные формы — один из самых причудливых и чудесных объектов в математике. Современный специалист по теории чисел Эйхлер причислил их к одной из пяти фундаментальных операций, т. е. умение обращаться с модулярными формами он считал настолько же важным, как и выполнение четырех действий арифметики. Надо сказать, что далеко не все математики уверенно чувствуют себя, сталкиваясь с этой пятой операцией, в отличие от первых четырех, где они считают себя мастерами.
Отличительной особенностью модулярных форм является их необычайно высокий уровень симметрии. Хотя большинство людей знакомо с повседневным понятием симметрии, в математике в термин «симметрия» вкладывают особый смысл. Объект считается обладающим симметрией, если его можно преобразовать дозволенным образом так, что преобразованный объект будет неотличим от исходного. Чтобы оценить необычайно высокую симметрию модулярной формы полезно сначала изучить симметрию какого-нибудь более знакомого объекта, например, простого квадрата.
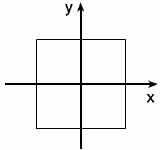
Рис. 18. Простой квадрат обладает вращательной и зеркальной симметриями
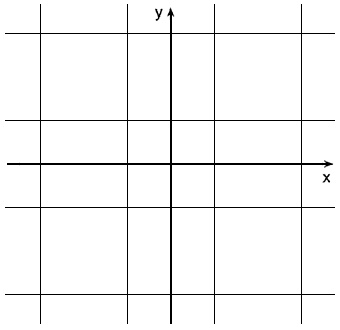
Рис. 19. Плоскость, выложенная квадратами, помимо вращательной и зеркальной симметрий обладает еще и трансляционной симметрией
В случае квадрата одна из форм симметрий — вращательная. Если мы мысленно проведем через точку пересечения осей x и y прямую, перпендикулярную рисунку, то квадрат на рис. 18 можно повернуть на четверть оборота — и он будет неотличим от исходного квадрата. Квадрат будет неотличим от исходного и после поворота на пол-оборота, три четверти оборота и полный оборот.
Помимо вращательной симметрии квадрат обладает зеркальной симметрией. Если представить себе, что зеркало расположено вдоль оси x перпендикулярно плоскости рисунка, то верхняя половина квадрата отразится точно на нижнюю и наоборот, поэтому после преобразования квадрат будет неотличим от исходного. Аналогично, мы можем поставить три других зеркала (вдоль оси y и двух диагоналей). Во всех случаях отраженный квадрат будет неотличим от исходного квадрата.
Простой квадрат симметричен, поскольку обладает вращательной и зеркальной симметриями. Но не обладает трансляционной симметрией. Это означает, что если квадрат подвергнуть сдвигу в любом направлении, то наблюдатель тотчас же заметит перемещение, поскольку положение квадрата относительно осей x и y изменится. Но если бы вся плоскость была вымощена квадратами, как на рис. 19, то этот бесконечный набор квадратов обладал бы трансляционной симметрией. При сдвиге такой разбитой на квадраты бесконечной поверхности на расстояние, равное одной или нескольким длинам квадрата, сдвинутая мозаика была бы ничем не отличима от исходной.
Симметрия выложенных плитками поверхностей — идея довольно простая, но, как это нередко бывает со многими простыми на первый взгляд понятиями, в ней скрыто немало тонкостей. Например, в 70-е годы британский физик и большой любитель занимательных задач-головоломок Роджер Пенроуз начал прикидывать различные варианты разбиения одной и той же поверхности на плитки различной формы. В конце концов он обнаружил две особенно интересные формы, которые он назвал воздушным змеем и дротиком (см. рис. 20). Каждая из этих форм сама по себе не годится для замощения всей поверхности без пробелов и наложений плиток друг на друга, но вместе воздушные змеи и дротики позволяют разбивать поверхность на мозаики с различным рисунком. Змеи и дротики можно сочетать бесконечным числом способов, и хотя рисунки мозаик кажутся похожими, они сильно отличаются в деталях. Одна из таких мозаик представлена на рис. 20.
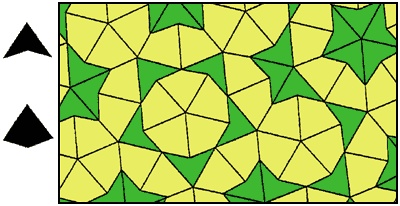
Рис. 20. Используя плитки двух различных форм Роджер Пенроуз сумел выложить ими всю плоскость. Однако мозаика Пенроуза не обладает трансляционной симметрией
Еще одна замечательная особенность мозаик Пенроуза заключается в том, что они обладает весьма ограниченным уровнем симметрии. На первый взгляд может показаться, что мозаика на рис. 20 обладает трансляционной симметрией, тем не менее любая попытка совместить мозаику с самой собой завершается неудачей. Мозаики Пенроуза оказались асимметричными, и этим они так привлекли математиков, что стали исходным пунктом в развитии целого нового направления.





