Птолемей усовершенствовал теорию эпициклов. Еще Гиппарх добавил в эту модель эксцентрические окружности: эпициклы равномерно движутся по большим окружностям деферентов, центры которых немного смещены относительно центра Земли. Это дополнение позволило ему достаточно точно описать наблюдаемое изменение скорости годичного движения Солнца. А Птолемей ввел следующее дополнение: эквант, точку внутри эксцентрической окружности. Центр эпицикла должен двигаться вдоль эксцентрической окружности с переменной скоростью, такой, чтобы для наблюдателя в экванте видимая угловая скорость оставалась постоянной. Эта уловка позволила в будущем лучше описывать движения планет. Однако она приводила к отказу от традиционного кругового движения. Позже Коперник, во всем остальном большой поклонник Птолемея, не мог признать эквант и остался верен идее равномерного кругового движения.
Размер сферической Земли.
Способы измерения астрономических расстояний своими корнями восходят к Фалесу, который, как утверждают, определял высоту пирамиды, дожидаясь момента, когда длина тени от вертикально стоящего шеста становилась равной длине самого шеста. В этот момент он измерял длину тени, отбрасываемой пирамидой. Это простая, но искусная процедура показывает, как сочетание наблюдений с математикой может привести к неожиданным результатам в изучении окружающего мира. Основы измерений космических расстояний были заложены в стране пирамид, в Александрии, где Эратосфен (около 275–195 до н. э.), хранитель библиотеки знаменитого Музея, измерил размер Земли, используя ее сферическую форму и, опять-таки, Солнце и тень.
Как географ, он собирался построить карту мира и нуждался в масштабе для ее координатной сетки. Его метод был очень прост: если известно расстояние между двумя точками, измеренное по искривленной поверхности Земли, и если известно угловое расстояние между ними, то можно прямо вычислить окружность Земли. Например, угловое расстояние от полюса до экватора равно одной четверти полной окружности, так что, умножив это расстояние на 4, мы получим длину окружности Земли.
Эратосфен взял две опорные точки: Александрию, где он жил, и Сиену (ныне Асуан), которые располагаются примерно на одной долготе (линия север-юг). Он знал, что в Сиене в день летнего солнцестояния в полдень исчезают тени, а значит, Солнце находится точно над головой. В это же время в Александрии Солнце расположено немного южнее зенита, поэтому тени видны. Угловое расстояние между этими двумя городами по его измерениям составляет около 7°, или 1/50 полной окружности в 360°. Следовательно, умножив линейное расстояние между Александрией и Сиеной 5 на 50, можно получить длину окружности Земли (схема измерений показана на рис. 3.4). Неизвестно, как Эратосфен определил расстояние 5, но он мог использовать время, которое требуется гонцу для преодоления этого пути. Так или иначе, он принял S = 5000 стадий и получил длину окружности Земли равную 250 000 стадий.
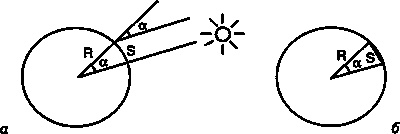
Рис. 3.4. (а) Схема измерения Эратосфена, где R — радиус Земли, S — расстояние от Александрии до Сиены, α — угловое расстояние Солнца от зенита в Александрии, а также угол при центре Земли. Большой круг — окружность Земли, (б) Схема триангуляции, где R — расстояние от наблюдателя до объекта, а — угловой размер объекта. Большой круг радиуса R с центром в точке наблюдения.
Стадия использовалась в соревнованиях греческих атлетов, но в ходу было несколько единиц с этим названием и разной длины. Мы точно не знаем, какую из этих единиц использовал Эратосфен, когда говорил о 5000 стадий. Короткая единица длиной 157,5 м (часто употребляемая историками) дала бы немного меньшее значение окружности Земли, а длинная единица в 185 м переоценила бы размер Земли: ее окружность имела бы длину либо 39 375, либо 46 250 км. Современное значение окружности Земли равно 39 942 км (полярное) и 40 075 км (экваториальное). Впрочем, здесь важно то, что еще в Античности, задолго до Колумба, были известны форма и размер Земли
[1]. Эратосфен показал, что можно измерить размер Земли, притом что увидеть ее целиком невозможно, используя измерения на поверхности и учитывая сферическую форму. Даже современные космологи применяют подобный способ для всей Вселенной.
Способ, которым Эратосфен измерил Землю, представляет собой частный случай триангуляции, использующий равнобедренный треугольник (с двумя равными сторонами). Как показано на врезке 3.2, в астрономии встречаются два подобных случая: когда базовой стороной треугольника служит размер далекого объекта, расстояние до которого мы определяем; либо когда базовая сторона находится «здесь», а далекий объект расположен в вершине треугольника.
Примером первого типа триангуляции может служить определение расстояния до Солнца, исходя из его углового размера (примерно полградуса). Если бы его истинный диаметр был бы известен, скажем, в километрах, можно было бы легко вычислить расстояние до него. Но даже в наше время мы не можем определить истинный размер с достаточной точностью, независимо от его расстояния. Не могли этого сделать и в древности. Анаксагор смело предположил, что Солнце — это светящийся камень размером с Пелопоннес (около 150 км). В этом случае метод триангуляции дает значение 17 000 км, тогда как правильное значение примерно в 10 000 раз больше (поскольку Солнце во много раз больше Пелопоннеса). Расстояние до Солнца никак не могли измерить в течение долгого времени, и только в XVII веке были сделаны довольно точные измерения.
Если базовая сторона «здесь», то она сама становится естественной единицей измерения, независимо от того, какова его длина в метрах или стадиях. С древности и до XVIII века радиус Земли служил основной единицей измерений в Солнечной системе. Как мы увидим ниже, расстояние Земля-Солнце используется как естественная база при измерении расстояний до ближайших звезд.
Врезка 3.2. Треугольники и расстояние.
Посмотрим на рис. 3.46. Если у нас равнобедренный треугольник (две стороны равны R), то, зная угол α при его вершине, между двумя равными сторонами, и длину базовой стороны S, мы легко можем вычислить высоту треугольника.
При астрономической триангуляции обычно астроном может измерить угол α, и, как правило, этот угол весьма мал, меньше нескольких градусов. Поэтому высота в треугольнике почти равна R.
Очертив воображаемую окружность радиусом R с центром в вершине треугольника, мы получим ту же картинку, что и Эратосфен, но в нашем случае R — это расстояние до объекта, а S — его физический размер. Длина воображаемой окружности равна S, деленной на ту часть, которую от 360° составляет угол α.
Расстояние R равно длине окружности, деленной на 2π. Обычно встречается два характерных случая.



