
Онлайн книга «Эволюция Вселенной и происхождение жизни»
Математические методы, необходимые для вычислений в неевклидовой геометрии, разработал Риман. Эта область математики, которую со временем изучил даже Эйнштейн, называется сейчас тензорным исчислением. Тензоры — это сложные величины, напоминающие векторы, которые используют для описания электрических полей. Примером тензора служит тензор кривизны, который описывает, насколько искривлено пространство, то есть насколько оно отличается от евклидова пространства. В четырехмерном пространстве тензор кривизны имеет 20 компонентов. Сравните это с вектором электрического поля, имеющим всего 3 компонента.
Еще в детстве Георг Риман (1826–1866) отличался выдающимися математическими способностями. К тому же он прилежно изучал Библию и в 1846 году, следуя отцовской воле, поступил в Гёттингенский университет на отделение теологии. Однако, посетив несколько лекций по математике, он попросил отца разрешить ему заняться математикой. Отец был не против, и Риман начал учиться математике, в том числе и у Гаусса. Под руководством Гаусса он завершил диссертацию и был взят на работу в Гёттингенский университет для подготовки к профессорскому званию (то есть — в аспирантуру). По окончании подготовки он выступил с лекцией «О гипотезах, лежащих в основании геометрии», которая теперь среди математиков считается классической работой. В ней обсуждается определение тензора кривизны и рассматривается вопрос о связи геометрии с миром, в котором мы живем. Какова размерность реального пространства и какой геометрией описывается наше пространство? Риман полагал, что само пространство может иметь измеряемые характеристики (рис. 15.2).

Рис. 15.2. Георг Риман — математик, проложивший путь для общей теории относительности.
Эта лекция намного опередила свое время и не была оценена большинством ученых. Согласно общепринятому тогда мнению, которое разделял и Ньютон, пространство служит жестким фоном, относительно которого проводятся все изменения. В окружении Римана только Гаусс смог оценить глубину мысли юного математика. На собрании факультета он с большой похвалой отозвался о профессоре физики Вильгельме Вебере и хвалил за оригинальность работу Римана.
Свойства неевклидовых геометрий.
Вселенная конечна или бесконечна? Это не так-то просто «увидеть». Евклидова геометрия прекрасно описывает наши обычные измерения. Но в будничной геометрии трудно встретиться с бесконечностью. С другой стороны, испытываешь немалые трудности, пытаясь представить себе конечный мир со сферической геометрией, хотя его конечность легко описывается математически.
Обычно для демонстрации неевклидовой геометрии в качестве примера используют поверхности. Наша трехмерная Вселенная (мы не учитываем время) в практическом отношении плоская, поэтому в ней мы легко можем заметить кривизну обычных поверхностей. Но трудно представить четырехмерное пространство, не разбираясь в том, что означает кривизна. Наш мозг не привык решать такие задачи, поэтому лучше ограничиться рассмотрением двумерных поверхностей. Сферическая Вселенная имеет странное свойство — у нее конечный объем, хотя ни в каком направлении невозможно найти ее край. Это легче понять, если представить поверхность сферы, которая позволяет нам заметить и другое интересное свойство сферической геометрии: идущий вперед путешественник вернется в начальную точку своего пути после того, как обойдет вокруг света. Путешествуя по Земле, если вы движетесь все время вперед по большому кругу, вы тоже вернетесь в исходную точку. Странный результат, если вы считаете Землю плоской!
Как легко понять, двумерным аналогом сферической Вселенной служит поверхность сферы. Не обязательно иметь возможность взглянуть на нее из третьего измерения или же обходить сферу кругом, чтобы догадаться о кривизне сферической поверхности. Существо, живущее на сферической поверхности, не способное выйти в третье измерение над этой поверхностью и даже не имеющее представления об этом третьем измерении, все равно может проводить построения на этой поверхности, чтобы узнать ее геометрические свойства. Оно может нарисовать треугольник и измерить сумму его внутренних углов. Если результат получится больше 180°, это докажет, что существо живет на сферической поверхности (рис 15.3). Или так: можно нарисовать круг и измерить его. Если отношение длины окружности к ее диаметру меньше, чем π (= 3,141592…), то существо будет знать, что оно живет в мире сферической геометрии.
В противном случае, если сумма внутренних углов треугольника меньше чем 180°, а отношение длины окружности к ее диаметру больше я и если через данную точку можно провести любое число линий, параллельных данной линии, то существо понимает, что оно живет в гиперболическом пространстве. Гиперболическое пространство тянется на бесконечное расстояние и не имеет аналога в обычной жизни. Форма седла, точнее — его центральной части, более или менее напоминает ограниченную область гиперболической поверхности.
Границей между сферическими и гиперболическими поверхностями служит плоская поверхность, или двумерное евклидово пространство. Привычные для нас законы евклидовой геометрии справедливы в этом и только в этом пространстве: сумма внутренних углов треугольника точно равна 180°, отношение длины окружности к ее радиусу в точности равно я, а через точку можно провести одну и только одну прямую, параллельную другой прямой (рис. 15.4).
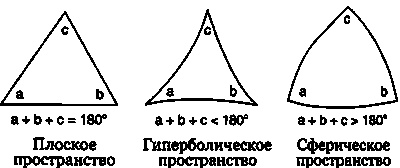
Рис. 15.3. Треугольники в плоском, гиперболическом и сферическом пространстве. Сумма углов в разных пространствах неодинакова.
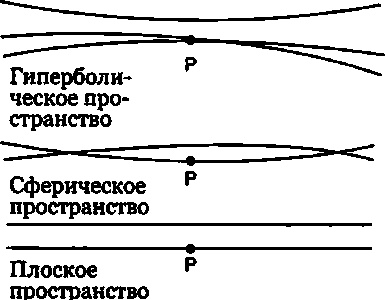
Рис. 15.4. Параллельные линии в разных пространствах. В плоском пространстве через данную точку Р можно провести только одну прямую, параллельную другой прямой. В гиперболическом пространстве можно провести любое количество таких прямых. В сферическом пространстве все прямые линии пересекаются, поэтому провести параллельную линию невозможно.
Значение кривизны пространства.
Математик Вильям Клиффорд (1845–1879) переводил труды Римана на английский язык и в процессе этой работы был очарован идеями Римана о связи между физическими явлениями и геометрией. Он стал развивать эти идеи. Читая лекцию в Кембриджском философском обществе, посвященную «науке о пространстве», он обсуждал нашу возможность судить о геометрии пространства на астрономических масштабах и на масштабах столь малых, что они недоступны для наблюдения (то есть в мире элементарных частиц). При этом он утверждал, что «малые области пространства фактически похожи на небольшие холмики на поверхности, которая в среднем плоская, таким образом, обычные законы геометрии к ним неприменимы». Он полагал, что «это свойство искривленности или искаженности непрерывно передается от одной области пространства к другой наподобие волны» и что «изменение кривизны пространства — это как раз то, что реально происходит в явлении, которое мы называем движением материи».
