Но можно определить расстояние и по-другому, непосредственно в тот момент, когда свет дошел до нас. Если использовать аналогию с воздушным шариком (см. рис. 23.5), то это будет расстояние между двумя точками, измеренное рулеткой по поверхности. Это расстояние легко можно сравнивать с расстояниями между современными галактиками. Оно дает нам представление о глубине пространства, на которой расположен объект. Например, оно говорит нам, сколько расстояний Галактика-Андромеда умещается в расстоянии между нами и далеким объектом. Такое определение расстояния довольно близко к тому, что мы обычно называем расстоянием. Впрочем, на самом деле мы не можем измерить это расстояние, протянув рулетку от нас до далекой галактики! Его можно только вывести из красного смещения этой галактики, используя подходящую фридмановскую модель. Как и при вычислении расстояния по времени распространения света, здесь тоже нужно знать красное смещение и иметь модель Вселенной. Мы видим, что космологическая модель — это не только теоретическая конструкция для описания и понимания Вселенной, но и практический инструмент, без которого невозможно говорить о расстояниях далеких небесных тел; а без расстояния мы не можем определить их размер и мощность излучения.
Таблица 23.2. Красное смещение, расстояние по времени распространения света и «расстояние сейчас».
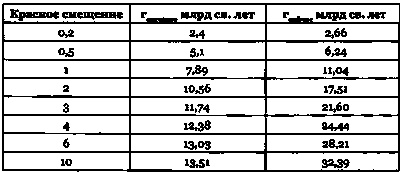
Эти расстояния рассчитаны по модели Фридмана при постоянной Хаббла = 70 км/с/Мпк, плоском пространстве, доле материи = 0,24 и доле темной энергии = 0,76.
Как пример возьмем галактику с красным смещением z = 2. Из табл. 23.2 мы видим, что свет покинул эту галактику около 10 млрд лет назад. Мы также можем вычислить, что в настоящее время она удалена от нас примерно в 7000 раз дальше, чем галактика Андромеда (расстояние до которой 2,5 млн световых лет). В этой таблице приведены расстояние по времени распространения света и «расстояние сейчас» по значению красного смещения. За единицу расстояния принят миллиард световых лет, и использована стандартная космологическая модель, в которой возраст Вселенной составляет 14 млрд лет.
Сейчас астрономы без труда наблюдают галактики до красного смещения около 0,5, что соответствует 64 % современного возраста Вселенной. С некоторыми трудностями удается наблюдать галактики при z = 3, это соответствует 16 % возраста Вселенной, а эпоха z = 10 была, когда от 14-миллиардного возраста мира прошло всего лишь 3,5 %.
Топология пространства: еще одна причина для головной боли.
Похоже, что плоские бесконечные модели Фридмана работают хорошо. Но мы хотим завершить эту главу рассказом об одном захватывающем предположении: может ли Вселенная быть плоской, но при этом конечной и содержать конечное число галактик?
Александр Фридман писал, что «распространены совершенно превратные сведения о конечности, замкнутости, кривизне и т. п. свойствах нашего пространства, которые будто бы устанавливаются принципом относительности… Я имею в виду пресловутый вопрос о конечности Вселенной, то есть о конечности нашего физического, занятого блистающими звездами пространства. Утверждают, что, найдя постоянную положительную кривизну Вселенной, можно якобы заключить о ее конечности и прежде всего о том, что прямая во Вселенной имеет «конечную длину», что объем Вселенной является тоже конечным и т. п.».
Он хотел подчеркнуть, что хотя в общей теории относительности кривизна пространства служит определяющей величиной, измерив ее, мы еще не узнаем глобальную форму и объем пространства. Отдельным вопросом является топология пространства. Напомним, что топология — это область математики, изучающая среди прочего особенности геометрических фигур и тел, которые не изменяются при растяжении или изгибе. В этом смысле, например, бублик и рамка от картины топологически эквивалентны. Так вот, топологию пространства невозможно вывести из общей теории относительности: нет простого, взаимно однозначного соответствия между кривизной пространства и его общей формой.
В процитированной выше книге «Мир как пространство и время», опубликованной в России в 1923 году, за два года до безвременной смерти, Фридман приводит педагогический пример. Двумерная геометрия поверхности цилиндра и геометрия плоскости одинаковы: обе поверхности — двумерные евклидовы пространства (рис. 23.8). Цилиндр можно склеить из плоского куска, и с нарисованным на плоскости треугольником ничего особенного не случится, если мы склеим друг с другом края этого куска. Сумма углов треугольника останется равной двум прямым углам, и теорема Пифагора, которая работает на плоскости, сохранит свою силу и на поверхности цилиндра.
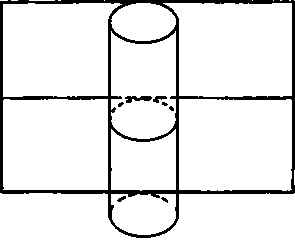
Рис. 23.8. Цилиндр можно изготовить из плоского прямоугольника. Поверхность цилиндра и плоскость обладают одинаковой внутренней евклидовой геометрией, но глобальная, то есть топологическая, структура у них совершенно разная.
Но в топологическом смысле это разные вещи: на цилиндре существуют «прямые линии конечной длины», тогда как на плоскости таких линий нет. Цилиндр имеет конечный размер в направлениях, перпендикулярных его оси, поэтому в этих направлениях он конечен и замкнут. Он бесконечен в направлении, параллельном его оси. Используя плоскость и цилиндр, Фридман приводит читателя к выводу: «Таким образом, одна метрика мира не дает нам никакой возможности решить вопрос о конечности Вселенной. Для решения этого вопроса нужны дополнительные теоретические и экспериментальные исследования».
После замечания Фридмана, сделанного в начале прошлого века о «дополнительных исследованиях», можно сказать, что до сих пор нет общей теории, связывающей топологию пространства-времени с его вещественным содержимым (математики говорят, что плоская, евклидова, геометрия может существовать у 18 топологически различных вариантов пространства!). Тем не менее можно приблизиться к решению этой проблемы путем наблюдений. Например, многочисленные изображения-«духи» одного и того же объекта могут наблюдаться на небе в топологически замкнутом пространстве конечного размера, потому что свет от яркого объекта может дойти до наблюдателя разными путями. Скажем, если лучи обогнут мир в разных направлениях, то мы можем увидеть один и тот же объект в двух диаметрально противоположных точках на небе. Но до сих пор такое не наблюдалось.
Замкнутая топология пространства должна была бы оставить свои следы и в виде «духов» фонового излучения. Первые наблюдательные свидетельства такого рода о топологии пространства обсуждал в 2003 году в Париже Жан-Пьер Люмине с коллегами. Они изучали топологическую информацию, содержащуюся в вариациях фонового излучения на предельно больших углах. Максимальным углом для вариаций обладает диполь. Но при угле в 180° невозможно получить данные, так как эффект Доплера, связанный с нашим движением относительно Вселенной (см. главу 24), тоже вызывает дипольный эффект, причем в 100 раз превышающий топологический. Максимальным наблюдаемым угловым масштабом вариаций обладает квадруполь с углом 90°. Последние данные WMAP показывают, что квадрупольные изменения составляют лишь одну седьмую от изменений, ожидаемых в бесконечном плоском пространстве. Для восьмиугольника с угловым масштабом 60° они составляют 70 % от ожидаемого в бесконечном пространстве. Для меньших угловых масштабов ослабления не наблюдалось.




