Но Вайнберг пошёл несколько дальше. Он заявил, что независимо от того, какой смысл вкладывается в антропный принцип и какой механизм обеспечивает его выполнение, одно достаточно ясно: принцип может показать нам, что λ должна быть достаточно мала, чтобы не убить нас, но нет никаких причин, по которым она должна быть в точности равна нулю. На самом деле нет никаких оснований и для того, чтобы она была намного меньше, чем это необходимо для обеспечения жизни. Не беспокоясь о глубинном смысле антропного принципа, Вайнберг по сути сделал важное предсказание: если антропный принцип является верным, то астрономы должны будут обнаружить ненулевую энергию вакуума, значение которой не будет существенно меньше, чем 10–120 Единиц.
Планковская длина
Меня всегда очаровывал процесс открытия. Я имею в виду психологию процесса, представляющего собой последовательность: цепь рассуждений – озарение – «Эврика!». Одно из моих любимых занятий – ставить себя на место какого-нибудь великого учёного и представлять, как бы я на его месте мог прийти к решающему открытию.
Сейчас я расскажу, как бы я внёс первый большой вклад в квантовую теорию гравитации. Это произошло бы за 16 лет до того, как молодой Эйнштейн создал современную теорию гравитации, и за 26 лет до того, как эти выскочки Гейзенберг и Шрёдингер придумали современную квантовую механику.
На самом деле я, Макс Планк, сделал это, сам того не осознавая.
Берлин, 1900 год. Институт кайзера Вильгельма
Недавно я сделал самое удивительное открытие: я открыл совершенно новую фундаментальную физическую константу. Люди называют её моим именем: постоянная Планка. Я сидел в своем офисе и думал: почему это у фундаментальных физических констант, таких как скорость света, гравитационная постоянная Ньютона и моя новая константа, такие неудобные значения? Скорость света составляет 2,997×108 метров в секунду. Гравитационная постоянная – 6,67×10–11 кубометров в квадратную секунду на килограмм. А моя константа – ещё хуже: 6,624×10–34 килограмм-квадратных метров в секунду. Почему они все такие большие или такие маленькие? Жизнь физиков была бы намного комфортнее, если бы все они были одного порядка.
И тут меня как ударило! Существуют три фундаментальные единицы для измерения длины, массы и времени: метр, килограмм и секунда. Есть также три фундаментальные константы. Если изменить единицы измерения, скажем, на сантиметры, граммы и часы, численное значение всех трёх констант изменится. Например, величина скорости света станет менее удобной: 1,08×1014 сантиметров в час. Но если я использую световые годы для измерения расстояния и годы для измерения времени, то скорость света будет равна в точности 1, поскольку свет проходит один световой год за один год. Не означает ли это, что я могу придумать несколько новых единиц измерения и сделать три фундаментальные константы такими, как мне удобно? Я даже могу найти такие единицы измерения, в которых все три фундаментальные физические константы будут равны единице! Это упростит множество формул. Я буду называть новые единицы измерения «естественными», поскольку они основаны на физических константах. Может быть, если мне повезёт, люди начнут называть их «планковскими единицами». Посчитать, срочно посчитать…
А вот и мой результат: естественная единица длины составляет около 10–33 сантиметра. Святой Бернулли! Это меньше, чем что-либо, о чём только можно подумать. Некоторые из тех, кто изучает атомы, говорят, что диаметр атома составляет около 10–8 сантиметра. Это значит, что новая естественная единица длины во столько же раз меньше атома, во сколько раз атом меньше Галактики!
[35]
Отлично! А что у нас с естественной единицей времени? Она получается порядка 10–42 секунды! Это невообразимо мало. Даже период колебания световой волны невообразимо больше естественной единицы времени.
А для единицы массы… Ага, естественная единица массы оказывается небольшой, но всё же не настолько малой: около 10–5 грамма. Примерно столько весит пылинка. Эти единицы должны иметь какое-то особое значение.
Все физические формулы выглядят значительно проще, если работать в естественных единицах. Интересно, что это значит?
Вот так Планк, сам того не осознавая, сделал одно из величайших открытий в области квантовой гравитации.
Планк прожил ещё 47 лет, дожив до 89. Но я не уверен, что он когда-либо представлял себе, сколь глубокое влияние оказали открытые им планковские единицы измерения на последующие поколения физиков. К 1947 году общая теория относительности и квантовая механика были частью базового курса физики, но едва ли кто-то думал о синтезе их в квантовую гравитацию. Три планковские единицы – единица длины, единица массы и единица времени – имели решающее значение для развития этой дисциплины, но даже сейчас мы только начинаем понимать всю их глубину. Я приведу лишь несколько примеров.
Ранее я уже говорил, что в теории Эйнштейна пространство растягивается и деформируется как поверхность воздушного шарика. Его можно растянуть в гладкую плоскость или скомкать, как старую газету. Но стоит совместить эту идею с квантовой механикой, как пространство обретает совершенно новые свойства. Согласно принципам квантовой механики, всё, что может колебаться, колеблется. Если пространство способно деформироваться, то оно должно быть подвержено «квантовой дрожи». Если бы у нас был очень мощный микроскоп, мы увидели бы, что пространство флуктуирует, вибрирует и мерцает, образуя в местах пучностей миниатюрные «бублики». Оно выглядело бы похожим на кусок ткани или бумаги. Издалека такой кусок выглядит ровным и гладким, но под микроскопом можно увидеть, что он полон ям, неровностей, волокон и отверстий. С пространством всё так же, только ещё хуже. Пространство не просто состоит из подобных текстур: эти текстуры ещё и невероятно быстро меняются.
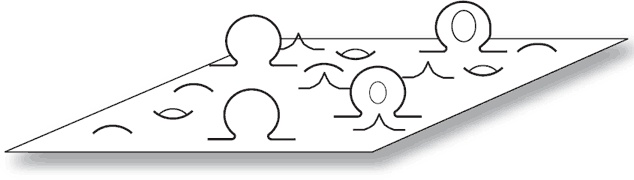
Насколько мощным должен быть микроскоп, чтобы показать нам флуктуирующую структуру пространства? Вероятно, вы уже догадались: микроскоп должен разрешать детали размером порядка планковской длины, то есть 10–33 сантиметра. Это и есть масштаб квантовой структуры пространства.
А как быстро меняется структура пространства на масштабе планковской длины? Опять же нетрудно догадаться, что характерный период этих флуктуаций должен иметь порядок планковского времени – 10–42 секунды!
Многие физики считают, что физический смысл планковской длины – это минимальное возможное расстояние. Аналогично, планковское время является кратчайшим возможным промежутком времени.
Но мы ещё не обсудили планковскую массу. Чтобы понять её физический смысл, представьте себе две частицы, сталкивающиеся с такой силой, что в результате они создают в точке столкновения чёрную дыру. Это действительно может случиться, если две сталкивающиеся частицы имеют достаточно большую энергию; в этом случае они исчезнут, оставив после себя чёрную дыру – один их тех загадочных объектов, о которых пойдёт речь в 11-й главе этой книги. Энергия, необходимая для формирования такой чёрной дыры, уже упоминалась ранее, когда я рассказывал об энергии вакуума. Насколько большой должна быть эта энергия, учитывая, что масса и энергия – это одно и то же? Ответ очевиден: разумеется, она должна быть равна планковской массе. Планковская масса не является ни минимальной, ни максимальной возможной массой частицы вещества; планковская масса – это минимальная возможная масса чёрной дыры. Кстати, чёрная дыра планковской массы будет иметь размер порядка планковской длины и просуществует не более планковского времени, прежде чем взорвётся, оставив после себя фотоны и прочий мусор.



