Нередко при определенной широте базы рассматриваемых вопросов возникают и побочные достижения. Работая над суперсимметрией, мы с Раманом Сандрамом получили в конце концов свернутое дополнительное измерение, позволяющее решить проблему иерархии. Потом мы еще раз внимательно посмотрели на уравнения, перенесли их на более широкий контекст и обнаружили, что бесконечное свернутое пространственное измерение может существовать, не порождая никаких противоречий с известными наблюдаемыми фактами или законами природы. Мы занимались физикой элементарных частиц — совершенно другой темой. Но одновременно мы старались удерживать в сознании и общую картину мира. Мы не забывали про глобальные вопросы о природе пространства даже тогда, когда наше внимание было поглощено частными моментами, такими как иерархия масштабов масс в Стандартной модели.
Важно, что ни Раман, ни я не были специалистами по теории относительности, так что к своим исследованиям мы подошли без всякой предвзятости. Ни нам и никому другому в голову бы не пришло, что теория гравитации Эйнштейна допускает существование невидимого бесконечного измерения, пока уравнения не показали нам, что это возможно. Мы упрямо разбирались в следствиях наших уравнений, не зная, что в кругах ученых, занятых теорией относительности, бесконечное дополнительное измерение считалось невозможным.
Тем не менее мы далеко не сразу щерились в том, что правы. Ни Раман, ни я не собирались слепо хвататься за радикальную идею. Выходить за пределы привычных пространства и времени имело смысл только после того, как мы и многие другие физики убедились, что традиционные идеи здесь не годятся. Хотя дополнительное измерение — достаточно свежая гипотеза, теория относительности Эйнштейна продолжает действовать. Поэтому мы могли воспользоваться готовыми уравнениями и математическим аппаратом, чтобы понять, как поведет себя наша гипотетическая вселенная.
Позже другие использовали результаты этого исследования и приняли модель с дополнительными измерениями за отправной пункт в собственных поисках новых физических идей, которые, возможно, будут применимы в какой‑нибудь вселенной без дополнительных измерений. Подойдя к этой проблеме буквально, физики увидели в ней возможности, которых прежде никто не замечал. Такой подход помог ученым выйти за рамки трехмерности.
Всякому, кто вторгается на новые территории, приходится мириться с массой неопределенностей — от них невозможно избавиться, пока проблема не будет решена полностью. Даже если вы начинаете с прочного фундамента существующих знаний, то, изучая новые явления, вы рано или поздно столкнетесь с неизвестностью и неопределенностью, хотя, конечно, рискуете вы при этом куда меньше, чем канатоходец. Не только космонавты, но и ученые, и художники дерзко стремятся «туда, где никто еще не бывал». Но их дерзость не слепа и не случайна, и они не пренебрегают достижениями предшественников, даже если речь идет о совершенно новых идеях и безумных экспериментах, которые, кажется, и реализовать‑то невозможно. Исследователи стремятся быть готовыми ко всему. Именно для этого нужны правила, уравнения и представления о непротиворечивости. Это страховка, которая защищает нас во время путешествия по неизвестным землям.
По словам моего коллеги Марка Камионковски, «хорошо быть амбициозным и смотреть в будущее». Но главное все‑таки — ставить реалистичные цели. Один студент, достигший больших успехов в изучении бизнес–менеджмента, заметил, что базой недавнего успешного экономического роста, раздувшегося затем в экономический пузырь, в значительной мере была именно креативность. Но, заметил он также, недостаток сдерживающих факторов привел к тому, что пузырь лопнул.
В качестве примера противоречивых намерений, которые внушают человеку уверенность и осторожность, можно привести даже самые важные открытия прошлого. Научный журналист Гэри Таубс однажды сказал мне, что ученые — одновременно самые уверенные и самые неуверенные люди на свете. Именно это противоречие гонит их все время вперед: с одной стороны, каждый из них уверен в том, что движется вперед, а с другой — самым жестким образом проверяет любые свои выводы. Творческий человек должен верить, что он может добиться многого, и при этом постоянно помнить о тех, у которых ничего не получилось.
Выдвигая смелые, подчас даже авантюрные идеи, ученые иногда очень неохотно представляют их миру. Известнейшие ученые Исаак Ньютон и Чарльз Дарвин много лет не решались поделиться с окружающими своими революционными идеями. Исследования Дарвина растянулись на десятилетия, и книга «Происхождение видов» вышла лишь после громадного количества наблюдений. Ньютоновы «Начала» представили теорию всемирного тяготения, на разработку которой у автора ушло больше десяти лет. Ньютон не публиковал трактат, пока не получил достаточных доказательств того, что тела произвольной геометрической формы (не только точечные) тоже притягиваются с силой, обратно пропорциональной квадрату расстояния. Именно в процессе доказательства этого закона Ньютон разработал методы дифференциального и интегрального исчисления.

РИС. 81. Задача: не отрывая карандаша от бумаги, соединить девять точек четырьмя отрезками прямой
Иногда требуется заново сформулировать проблему, чтобы увидеть ее в новом свете и заново определить границы, а затем найти решение там, где на первый взгляд никакого решения и быть не может. Для успеха начатой работы нередко очень важны упорство и вера — не в бога, а в то, что решение все‑таки существует. Истинные ученые — и вообще творческие люди — никогда не останавливаются, оказавшись в тупике. Если проблема не решается одним способом, они пробуют решить ее иначе. Если впереди непреодолимое препятствие, они роют тоннель, ищут другое направление или поднимаются в воздух и составляют карту местности. Именно здесь вступает в игру воображение. Чтобы продолжать, мы должны верить в то, что ответ реально существует, а мир изначально логичен, и эту логику мы в конце концов обязательно обнаружим. Посмотрев на проблему под верным углом, можно заметить связи, которые в противном случае обязательно пропустишь.
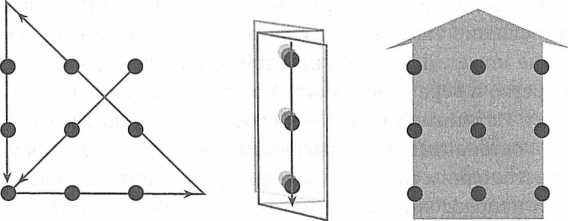
В качестве иллюстрации можно привести известную задачу, в которой требуется, не отрывая карандаша от бумаги, соединить девять точек четырьмя отрезками прямой (рис. 81). Если держаться в пределах образованного точками квадрата, решения у задачи не существует, но ведь никто не задавал вам такого ограничения! Стоит выйти за пределы квадрата, и решение появляется (рис. 82). В этот момент вам, возможно, придет в голову, что проблему можно переформулировать еще несколькими способами. Если точки будут большими, можно ограничиться тремя линиями. Если сложить бумагу (или воспользоваться очень широким пером, как предложила создателю задачи одна маленькая девочка), хватит и одной линии.