«Если мы сможем теперь объяснить состояние тела по отношению к окружающему веществу, когда говорится, что оно «заряжено» электричеством, и объяснить силы, действующие между наэлектризованными телами, то мы сможем тем самым установить связь между всеми феноменами электрической науки» (Maxwell, [1861], p. 13).
Далее, отмечает Максвелл, если существует разница в натяжениях между различными частями любого тела, то электричество протекает, или стремится протечь, от мест с большим натяжением к местам с меньшим натяжением. Если рассматриваемое тело – проводник, будет иметь место действительное прохождение электричества.
Но если перед нами изолятор, то, несмотря на то, что электричество течь по нему не может, электрические эффекты и их распространение все же могут иметь место. В данном отношении проводник может быть уподоблен пористой мембране, которая оказывает сопротивление прохождению жидкости через нее; в то время как диэлектрик аналогичен эластичной мембране, которая для жидкости непроницаема, но позволяет передавать давление из одной части в другую.
Действующая на диэлектрик электродвижущая сила поляризует его части подобно поляризации железных опилок под воздействием магнита, приводя к тому, что каждая железная частица становится обладательницей двух полюсов, направленных в противоположные стороны. Поэтому в диэлектрике под воздействием индукции электричество в каждой молекуле смещается таким образом, что одна сторона оказывается заряженной положительно, а другая – отрицательно. Тем не менее, электричество всецело остается в пределах молекулы, и не перетекает от одной молекулы к другой.
«В результате этого воздействия на весь диэлектрик возникает общее смещение электричества в определенном направлении. Это смещение не доходит до тока, поскольку, как только оно достигнет определенного значения, оно остается постоянным, но это – начало тока…» (Maxwell, [1861], p. 14).
В итоге если h – смещение, R – электродвижущая сила, а E – коэффициент, зависящий от природы диэлектрика, то R = – 4πE h. Величина электрического тока из-за смещения r будет определяться из выражения:
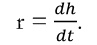
Эти соотношения не зависят ни от какой теории внутреннего механизма диэлектриков; но когда мы найдем электродвижущую силу, образующую электрическое смещение в диэлектрике, и когда мы найдем диэлектрик, освобождающийся от его состояния электрического смещения с равной электродвижущей силой, тогда мы придем к сравнению этого явления с упругим телом, которое поддается давлению и возвращает первоначальную форму тогда, когда давление устранено (Maxwell, [1861], p. 14).
Для дальнейшего изложения существенно следующее замечание Максвелла, сделанное им в процессе развертывания теории молекулярных вихрей.
«В последующем я рассмотрел отношение между смещением и той силой, которая его производит, в предположении, что ячейки являются сферическими. Действительная форма ячеек возможно [!] не настолько значительно отличается от сферической для того, чтобы привести к большим отличиям в численном результате» (Maxwell, [1861], p. 14).
Этот результат был необходим Максвеллу «для получения соотношения между статической и динамической мерами электричества, и показал, при помощи сравнения электромагнитных экспериментов М. М. Кольрауша и Вебера со скоростью света, найденной М. Физо, что эластичность магнитной среды в воздухе – та же самая, что эластичность светоносной среды, если только эти две сосуществующие, одинаково протяженные и одинаково эластичные среды не одна и та же среда» (Maxwell, [1861], p. 14).
Введение тока смещения потребовало изменения системы уравнений, полученных Максвеллом ранее, что и выразилось в доказательстве следующей теоремы (proposition XIV): скорректировать уравнения для электрических токов [уравнения (9) в обозначениях Максвелла] с учетом эластичности среды. Продифференцировав приведенное выше выражение для электродвижущей силы смещения по t, получим выражение
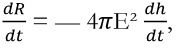 показывающее, что когда электродвижущая сила изменяется, электрическое смещение также изменяется. Но изменение смещения эквивалентно току, и этот ток должен быть добавлен в правую часть полученного ранее закона Ампера. В итоге три (x,y,z) компоненты вектора тока будут выглядеть следующим образом:
показывающее, что когда электродвижущая сила изменяется, электрическое смещение также изменяется. Но изменение смещения эквивалентно току, и этот ток должен быть добавлен в правую часть полученного ранее закона Ампера. В итоге три (x,y,z) компоненты вектора тока будут выглядеть следующим образом:
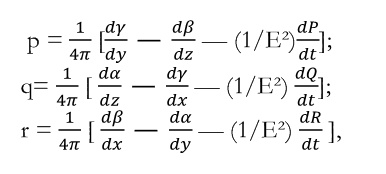
где p, q, r – это компоненты вектора электрического тока в направлениях x,y,z; α, β, γ – компоненты вектора магнитного поля, а P, Q, R – компоненты электродвижущей силы. Тогда, если e – количество свободного электричества в единице объема, то уравнение непрерывности будет выглядеть следующим образом:
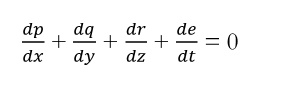
Продифференцировав полученное выше выражение для p,q,r по x,y,z и подставив результаты в уравнение непрерывности, получим:
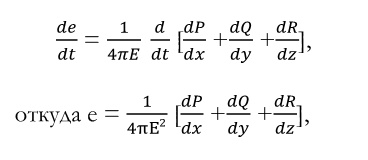
Последняя формула нужна Максвеллу для того, чтобы доказать следующую теорему (proposition XV): найти силу, действующую между двумя наэлектризованными телами. Используя выражения для энергии, возникающей в среде в результате смещения, а также соответствующие выражения для электрического напряжения, Максвелл получает
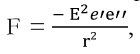 т. е. искомая сила есть отталкивание, изменяющееся обратно пропорционально квадрату расстояния между двумя наэлектризованными телами.
т. е. искомая сила есть отталкивание, изменяющееся обратно пропорционально квадрату расстояния между двумя наэлектризованными телами.
Таким образом, распространение теории молекулярных вихрей на явления электростатики оказалось возможным именно из-за учета упругости вихрей, которые делают магнито-электрическую субстанцию способной поддерживать волны упругости.
Определенная ранее в теореме XIII величина E оказывается коэффициентом, на который должно быть умножено выраженное в магнитных единицах количество электричества для того, чтобы получить число, выражающее то же самое количество электричества, но в электростатических единицах. Вебер и Кольрауш нашли, что E = 310 740 000 000.
Все это необходимо Максвеллу для того, чтобы доказать теорему XVI: найти скорость распространения поперечных колебаний через упругую среду, из которой состоят ячейки, в предположении, что ее упругость целиком обусловлена силами, действующими между парами материальных точек.



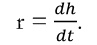
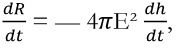 показывающее, что когда электродвижущая сила изменяется, электрическое смещение также изменяется. Но изменение смещения эквивалентно току, и этот ток должен быть добавлен в правую часть полученного ранее закона Ампера. В итоге три (x,y,z) компоненты вектора тока будут выглядеть следующим образом:
показывающее, что когда электродвижущая сила изменяется, электрическое смещение также изменяется. Но изменение смещения эквивалентно току, и этот ток должен быть добавлен в правую часть полученного ранее закона Ампера. В итоге три (x,y,z) компоненты вектора тока будут выглядеть следующим образом: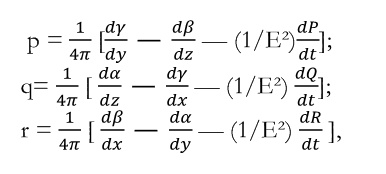
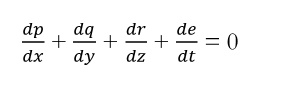
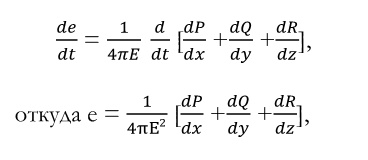
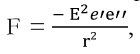 т. е. искомая сила есть отталкивание, изменяющееся обратно пропорционально квадрату расстояния между двумя наэлектризованными телами.
т. е. искомая сила есть отталкивание, изменяющееся обратно пропорционально квадрату расстояния между двумя наэлектризованными телами.