Юноша знает не только законы [...], но и французский, латынь, греческий, иврит, сирийский и халдейский; он прекрасный математик, музыкант и художник.
Из письма Константина графу Нассау-Зигенскому
По иронии судьбы, болезнь помогла Христиану выйти из тупика. В Европе XVII века оспа была практически обязательным заболеванием, которого не могли избежать даже высшие слои общества. Осенью 1650 года Вильгельм II, только что одержавший верх над своими политическими противниками, умер от вируса, так и не увидев своего единственного сына, который родился через восемь дней после его смерти. Сторонники республики постарались воспользоваться периодом регентства для уничтожения наследной монархии. Преданность Оранской династии закрыла семье Гюйгенсов дорогу к высоким постам. Они оказались специалистами в деле, которым больше не могли заниматься. Для Константина это стало тяжелым ударом, однако его сыновья перенесли удар судьбы гораздо легче. Константин дал старшему сыну передышку. Пока молодой наследник престола, будущий Вильгельм III, подрастал, брат Христиана пил, рисовал и растрачивал свое блестящее образование в общении с прекрасным полом. Христиан же наконец смог спокойно заняться наукой.
ПЕРВЫЕ ИССЛЕДОВАНИЯ
Благодаря ван Схотену Гюйгенс прекрасно владел математикой, существовавшей до появления математического анализа. Первых успехов он добился в геометрии, в тех ее областях, которые сегодня считаются устаревшими: такие как квадратура — геометрическая игра, состоящая в том, чтобы строить квадраты на основе любых фигур так, чтобы площадь квадрата была равна площади исходной фигуры. При решении задачи можно было пользоваться только линейкой и циркулем, из-за чего построить некоторые квадратуры, например квадратуру круга, было невозможно. Только в XIX веке немецкий математик Фердинанд фон Линдеман доказал невозможность такого построения, но до этого момента лучшие умы посвящали поискам решения огромное количество сил и времени. В возрасте 22 лет Гюйгенс нашел ошибку в одной из самых сложных попыток, предпринятой фламандским иезуитом Грегорио ди Сан Винченцо. Христиан усовершенствовал метод построения квадратур и применил его к коническим сечениям (эллипсам, параболам и гиперболам), а с помощью приблизительной квадратуры круга улучшил метод Архимеда для вычисления цифр после запятой в числе π.
Ван Схотен с энтузиазмом отнесся к работам Гюйгенса и полагал, что их можно поставить в один ряд с трудами древних греков. Он был прав, однако в XVII веке в математике происходила резкая смена вектора, окончательно отделившая ее от древнегреческой науки. Несмотря на то что геометрические открытия Гюйгенса не оставили заметного следа в истории математики, благодаря им он заслужил восхищение современников, а также овладел инструментами, позволявшими понять механизм природы.
Гюйгенс разделял интерес Архимеда к механике. На страницах трудов обоих соседствуют треугольники, весы, параболы и центры притяжения, так что трудно сказать, где заканчивается физика и начинается математика. В нидерландском языке есть слово vernufteling, как нельзя более точно описывающее Гюйгенса. Оно обозначает одновременно отличные интеллектуальные способности и склонность к ручному труду. Ученый не создал грандиозных систем, как Декарт или Ньютон, его больше интересовали отдельные явления, которые он разбирал так, словно имел дело с шестеренками сложного механизма, только вместо гаечных ключей и отверток использовал алгебру и геометрию. Все увлечения Гюйгенса приводили к изобретениям (таким как телескопы и часы), рождавшимся из почти чудесного объединения физики, математики и тонкого ручного труда. Ученый был любопытным примером стремления к чистой абстракции и одновременно с этим — ремесленного прагматизма. Это сочетание очень рано проявилось в его работе в области оптики. Свойства линз со временем стали главным научным интересом Гюйгенса, которому он отдавался на протяжении всей жизни, в итоге усовершенствовав конструкцию телескопа, а также сделав удивительные астрономические открытия. А самое главное — благодаря этому интересу ученый совершил одно из глубочайших исследований природы света. Конец истории имел для Гюйгенса горьковатый привкус: в соперничестве с Ньютоном они находились в разных весовых категориях, но в самом начале научной дуэли, когда Христиан дошел до пределов Солнечной системы, он, без сомнения, одержал победу.
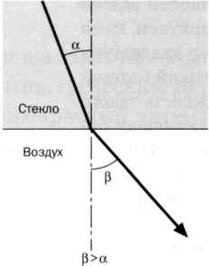
РИС. 1
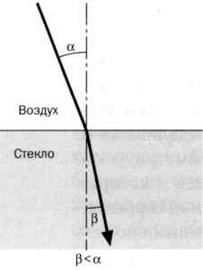
РИС. 2
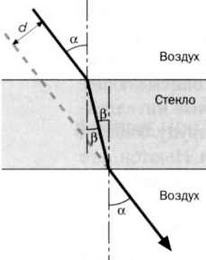
РИС.З
ЛАБИРИНТЫ СВЕТА
В конце октября 1652 года Гюйгенс признавался ван Схотену: «Я полностью поглощен диоптрикой». Этим термином в 1611 году Кеплер обозначил область, математически исследующую траектории луча света при прохождении через группу линз. Непротиворечивая теория, способная объяснить все явления, связанные с взаимодействием света и материи, появилась только в XX веке. Но для создания оптических инструментов достаточно воспользоваться приближением геометрической оптики, в рамках которого свет рассматривается как пучок прямых линий. Ниже мы постараемся объяснить, в каком состоянии находилась диоптрика до того, как ею занялся Гюйгенс.
Свет преломляется или отклоняется, пересекая границу двух сред, которые в состоянии пропустить его. При этом часть света отражается — этот аспект мы не будем принимать во внимание, но он ограничивает количество линз, которые можно разместить в одной оптической системе. Чем больше стекол должен пересечь свет, тем больше его потеряется по пути и тем слабее будет изображение.
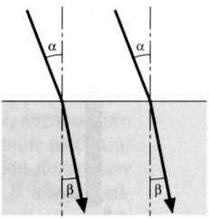
РИС. 4
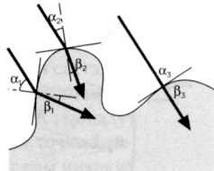
РИС. 5
Явление рефракции можно наблюдать в любой прозрачной среде, когда солнечные лучи проходят через воду, воздух и стекло. Угол отклонения зависит от каждой пары сред. Так, если луч проходит от стекла к воздуху (см. рисунок 1), угол будет больше (β > а), а если в обратном направлении, от воздуха к стеклу (см. рисунок 2), то меньше.
Проходя через прозрачное тело, лучи света дважды пересекают границу сред, то есть дважды преломляются. Если эти границы являются плоскими и параллельными друг другу, при отклонении лучи смещаются в сторону (d), как в случае с оконным стеклом (см. рисунок 3).







