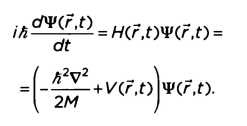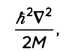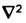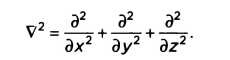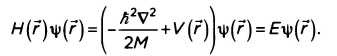УРАВНЕНИЕ ШРЁДИНГЕРА

В теории Шрёдингера состояние квантовой системы определяется через сложную математическую функцию, называемую волновой функцией Ψ, которая зависит от времени и всех координат, определяющих наблюдаемую систему. Уравнение Шрёдингера представляет собой дифференциальное уравнение первого порядка. Оно включает зависимость от времени, которая выглядит следующим образом:
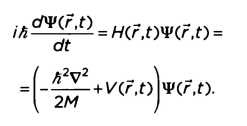
Переменная Н является функцией Гамильтона, которая включает в себя всю информацию об общей энергии системы — кинетической и потенциальной. Кинетическая энергия (связанная с движением) определяется дробью
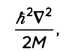
где М является массой системы, а
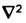
— оператором Лапласа:
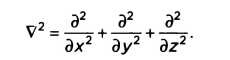
Наконец, величина V(ŕ,t) означает потенциальную энергию. Когда гамильтониан не зависит от времени, уравнение Шрёдингера может быть решено через определение того, что мы называем «стационарными состояниями». Независимое от времени уравнение Шрёдингера позволяет определить волновую функцию, зависящую от пространственных переменных:
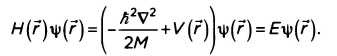
В данном случае (то есть в стационарном состоянии) гамильтониан, действуя на волновую функцию, выражает общую энергию системы. Иначе говоря, энергия Е составляет собственную величину гамильтониана. Уравнение Шрёдингера несовместимо с теорией относительности. Мы увидим, что способ введения пространственно-временных переменных в уравнение разнится. Если время появляется как производная первого порядка, то пространственные координаты выражаются производными второго порядка. Этот аспект противоречит неотъемлемому принципу теории относительности — симметричному обращению с четырьмя составляющими (тремя пространственными составляющими и одной временной), которые образуют «четырехмерный вектор пространство — время».
«Сначала я испытал некоторую враждебность по отношению к теории Шрёдингера. Зачем надо было возвращаться к состоянию, предшествовавшему Гейзенбергу, если уже была квантовая механика? Меня глубоко беспокоил риск возврата назад и, возможно, забвения всего прогресса, осуществленного квантовой теорией. На протяжении некоторого времени я испытал настоящую враждебность по отношению к идеям Шрёдингера».
Доказательством полного отсутствия интереса к формализму Шрёдингера служит тот факт, что Дирак никак не упомянул о нем в диссертации, которую представил в мае 1926 года.
Несмотря на сдержанность Дирака, волновую механику ждал огромный успех, большинство физиков того времени были рады забыть сложный и непонятный язык матриц и q-чисел ради простоты дифференциального уравнения Шрёдингера. В серии статей, опубликованных весной-летом 1926 года, Шрёдингер сформулировал основы своей новой теории, учитывающей энергетические уровни атома водорода. У него вся информация о системе заключалась в «волновой функции» — сложной математической функции, значение которой тогда не было очевидным.
Язык Шрёдингера сильно отличается от языка, используемого Гейзенбергом, Борном и Йорданом, а также Дираком. Это расхождение в теориях, описывающих и объясняющих одни и те же природные явления, особенно трудно было принять Дираку, который всегда пытался найти последовательное и единое описание субатомного мира. Физическую интерпретацию волновой функции дал Борн летом 1926 года. Сегодня она известна как «вероятностная интерпретация». Согласно ей «плотность вероятности нахождения частицы характеризуется квадратом волновой функции». Что касается соотношения обеих теорий — волновой и матричной механики, — сам Шрёдингер доказал их математическую эквивалентность в третьей статье. Похоже, Паули доказал это немного раньше, хотя ничего на данную тему не опубликовал.
ДИРАК И ВОЛНОВАЯ МЕХАНИКА
Доказательство математической эквивалентности волновой и матричной теории, или алгебры q-чисел, развеяло все сомнения, которые Дирак еще мог испытывать по поводу нового формализма. С тех пор ученый занял очень прагматичную позицию и признал, что некоторые проблемы значительно легче решаются с помощью волновой механики.
Так, очень скоро Дирак опубликовал новую статью под названием «О теории квантовой механики», в которой впервые использовал волновую теорию и применил ее к системам тождественных частиц.
Что такое «тождественные частицы» в квантовой теории и в чем именно состоит вклад Дирака? Чтобы ответить, нам надо ненадолго вернуться в предыдущий 1925 год и задаться другим вопросом: почему мы можем объединять химические элементы в определенные группы по их химическим свойствам? Паули объяснил, что химические свойства являются следствием того, каким образом электроны располагаются на соответствующих орбитах. Каждый электрон описывается серией квантовых чисел, характеризующих волновую функцию. Эти квантовые числа определяют энергию электрона, его орбитальный момент и новое свойство, которое пришлось ввести для объяснения результатов последних опытов, — «спин» (мы подробно рассмотрим его в следующей главе). Паули сформулировал следующий принцип:
«Два электрона не могут находиться в одном квантовом состоянии, то есть они не могут иметь одну и ту же совокупность квантовых чисел».
Данный принцип объяснил, почему атомные электроны располагаются на разных орбитах, занимая только те, которые свободны. На самом деле принцип Паули позволяет понять, почему вещество является таким, какое оно есть.
Другим важным свойством квантового мира является то, что мы не можем различить тождественные частицы. В классической физике положение частицы и ее состояние движения настолько прекрасно определяются, что даже при большом количестве частиц можно узнать, какое положение занимает каждая из них. Напротив, в квантовом мире положение четко определить невозможно и, соответственно, в случае с двумя электронами (назовем их a и b) и двумя квантовыми состояниями (m и n) невозможно узнать, в каком именно состоянии находится каждый электрон. На самом деле ситуация, соответствующая электрону a в состоянии m (обозначим ее am) и электрону b в состоянии n (bn)> имеет такую же вероятность, как и обратная комбинация, an,bm. Если использовать более техническую терминологию, обе комбинации представляют одно и то же квантовое состояние и таким образом должны быть пропорциональны, с коэффициентом пропорциональности +1 или -1. Добавим, что если мы поменяем два раза подряд положение двух электронов, то полученная комбинация должна быть тождественна изначальной комбинации.