Эти техники дали возможность переформулировать теорию квантовой электродинамики, превратив ее в самую точную физическую теорию.
Новая теория Дирака была принята довольно сдержанно и вызвала резкую критику со стороны его коллег. Паули находил идеи Дирака «искусственными, математически слишком сложными и лишенными физического смысла». Обычно сдержанный Гейзенберг высказался еще резче, расценив теорию как абсурдную. Понятие поляризации вакуума, введенное Дираком, однако закрепилось, и очень скоро другие ученые начали изучать этот эффект.
Сообщество физиков было озадачено и в основном испытывало чувство неудовлетворения. Сам Дирак становился все более скептичным, и по сути его мнение не отличалось от мнения Гейзенберга и Паули. Он попытался решить проблему бесконечных величин, используя сложные и «искусственные» математические техники, вопреки «математической красоте физики» (а следование ей было самым дорогим ему принципом). В последующие годы разочарование Дирака достигло такой степени, что он пошел еще дальше своих коллег в критике квантовой электродинамики.
ПРОБЛЕМА БЕСКОНЕЧНЫХ ВЕЛИЧИН И ПЕРЕНОРМИРОВКА
Проблема результатов с бесконечными пределами и расходящихся интегралов уже появлялась в XIX веке в связи с электромагнитной теорией Максвелла. Электрически заряженная частица порождает вокруг себя поле, которое в свою очередь производит электромагнитную энергию, меняющую массу частицы («собственная энергия»). Эта энергия обратно пропорциональна расстоянию между положением заряженной частицы и положением, в котором вычисляется энергия поля. Трудность заключается в следующем: какую энергию производит электромагнитное поле, образованное частицей в ее собственном положении? Логически расстояние равно нулю, что влечет за собой результат в виде бесконечной величины. С классической точки зрения проблема решена, так как частица имеет определенную структуру и конечное расширение, поскольку заряд распределен по ее поверхности. Поэтому энергия, произведенная полем, обратно пропорциональна радиусу, определяющему расширение частицы.
В квантовой физике не допускается представление об электроне с пространственным расширением; напротив, электрон является элементарной частицей, без внутренней структуры. Квантовое описание электрического поля, образованного электроном, задано через испускание или поглощение виртуальных фотонов, существование которых вытекает из принципа неопределенности Гейзенберга. Этот процесс изображен на рисунке 1. Такие графики называются «диаграммами Фейнмана». В определенный момент электрон, представленный непрерывной линией, испускает фотон, который затем вновь поглощается самим электроном (траектория фотона соответствует волнистой линии). Расчет данного процесса (вычисление собственной энергии электрона) ведет к появлению расходящихся интегралов. Описанный процесс соответствует самому простому случаю, когда испускается и поглощается только один фотон. Но можно представить гораздо более сложные процессы, увеличивая количество вовлеченных виртуальных фотонов.

РИС. 1
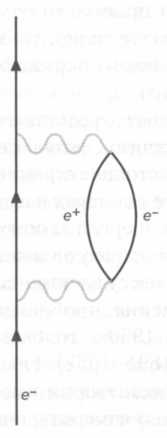
РИС. 2
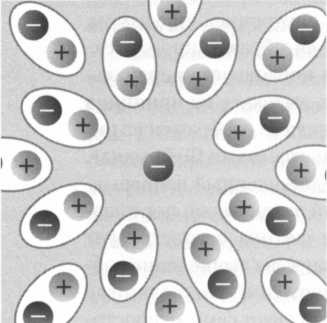
РИС. 3
Сочетание принципа неопределенности и принципа эквивалентности массы и энергии является главным для понимания квантового вакуума. В квантовом вакууме непрерывно происходят квантовые колебания, которые могут привести к рождению виртуальных пар частица/античастица. Введенное Дираком понятие поляризации вакуума напрямую связано с этими виртуальными парами. Рассмотрим электрон, непрерывно испускающий и поглощающий виртуальные фотоны, которые в свою очередь могут приводить к рождению виртуальных пар электрон/позитрон. Позитроны стремятся приблизиться к физическому электрону, тогда как виртуальные электроны стремятся удалиться от них (см. рисунок 2).
Этот процесс тоже может быть показан через диаграммы. В результате видно, что заряд электрона частично нейтрализуется «облаком» окружающих его виртуальных позитронов (см. рисунок 3).
Процесс, представленный на предыдущих рисунках, может быть рассчитан; результат с бесконечным пределом появляется, когда расстояние стремится к нулю. Важно заметить, что анализ все более коротких расстояний приводит к рассмотрению все больших энергий, и поэтому бесконечное количество все более сложных процессов может значительно влиять как на энергию, так и на массу электрона.
Решение проблемы бесконечных величин появилось в конце 1930-х годов вместе с работами Хендрика А. Крамерса (1894-1952). Главная идея заключалась в следующем: в квантовой теории имеют смысл только те величины, которые можно измерить; иначе говоря, величины, которые невозможно измерить, определять не имеет смысла, они могут быть неопределенными. Так, масса и заряд электрона, наблюдаемые в лаборатории, соответствуют действительному электрону, то есть электрону, испускающему и поглощающему виртуальные фотоны, непрерывно поляризуя вакуум. Зато величины, появляющиеся в уравнениях квантовой электродинамики, соответствуют массе и заряду электронов, которые не подвергаются взаимодействию (обычно называемые идеальными или голыми электронами). Между тем эти величины «голых» электронов (m0,е0) могут быть неопределенными (бесконечными), поскольку они соответствуют не физической ситуации. В реальности действительный электрон всегда является объектом взаимодействия: даже если он изолирован, он взаимодействует сам с собой, испуская и поглощая фотоны.
В конце 1940-х годов Фейнман, Швингер и Томонага разработали математический метод, позволяющий получить однозначные результаты. Он называется «методом перенормировки» и устанавливает отношение между измеренными в лаборатории значениями массы и заряда электрона и «возможными» значениями, соответствующими «голому» электрону. Данное отношение задано через постоянные перенормировки.
Как определить эти постоянные для физических результатов таким образом, чтобы они не были двусмысленными? Процедура, разработанная Ричардом Фейнманом, заключалась во введении числа минимального вычитания в решениях различных интегралов так, чтобы их результат и, соответственно, значения «голого» электрона имели конечный предел. Однако проблема состоит в том, что эти значения во многом зависят от выбранного числа вычитания. Иначе говоря, свойства «голого» электрона по-прежнему не определены.
Особенно интересно, что полученные в результате этого процесса «голые» значения, полностью зависящие от числа вычитания, всегда соответствуют физическим результатам — при условии, что исчисление физических свойств электрона включает все то, что предварительно было учтено при определении «голых» значений. Другими словами, число вычитания влияет только на определение «голых» значений — теоретических чисел, которые прямо наблюдать нельзя. Как бы там ни было, несмотря на неоспоримый шаг вперед в развитии квантовой электродинамики, сам Фейнман считал операцию перенормировки «слегка безумной».





