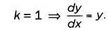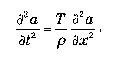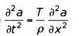Возьмем самый простой случай:
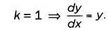
Теперь, как можно увидеть из уравнения, касательная пропорциональна значению функции в каждой точке. Решение у(х) = ех представлено на рисунке.
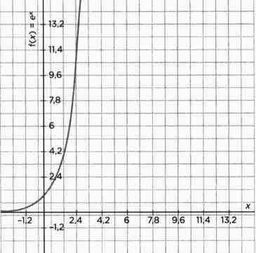
Несколько значений функции:
у(0) = е0 = 1
у(1) = е1 = 2,72
у(2) = е2 = 7,39
у(3) = е3 = 20,09
На самом деле мы констатируем, что у быстро возрастает при увеличении значения х и что у заставляет свою касательную принять такую же динамику (рисунок напротив).
Начиная с XVII века математический механизм, изучавший свойства функций и их производных, стали использовать в физике для прогнозирования, и этот способ предсказания до сих пор был неизвестен в истории науки. Физические соображения выражались в уравнениях, и математика давала ответ на вопрос, где будет располагаться планета Марс через пять столетий или пуля через долю секунды.
При попытке решить физические задачи использовались все грани анализа. Математики шли все дальше в джунгли дифференциальных уравнений, ведь там их ждали открытия.
Одним из первых их любопытство пробудило волновое уравнение. С реальностью его сближала музыкальная теория, поскольку уравнение описывало колебания струны, натянутой между подставкой и колками. Уравнение описывало поведение струны после прикосновения. Применение законов Ньютона вело к следующему выражению с частичными производными:
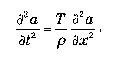
где р и Т— две постоянные (линейная плотность струны и сила, на нее воздействующая) и где а — пространственная и временная функция, соответствующая вертикальному расстоянию, отделяющему каждую точку струны от горизонтальной плоскости (рисунок 12).
Это уравнение допускает бесконечное множество решений. Некоторые из них приемлемы для математиков, но теряют физический смысл и потому отбрасываются; другие не удовлетворяют некоторым дополнительным условиям, к примеру тому, что концы струны никогда не колеблются, что струна остается неподвижной до того момента, пока ее не коснутся или пока она не приобретет определенную форму Эти требования сокращают диапазон приемлемых решений, но также они квантифицируют значение частоты (v), с которой колеблется струна. При прикосновении к концам струны решениями являются волны, которые свободно распространяются по струне слева направо. Они могут это делать с любой частотой: тогда v является постоянной величиной. Однако при фиксации струны волны останавливаются между двумя краями, v прерывается и становится дискретной переменной. Диапазон ее значений кратен фундаментальной частоте, v1 звучание струны при этом может приближаться (через р и Т) к чистой музыкальной ноте (рисунок 13).
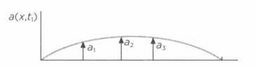
РИС. 12

РИС. 13
Эти колебания называются стоячими волнами: в каждой их точке колебания происходят с той же частотой, что и у встречных волн. Волны свободно распространяются вдоль струны влево или вправо, затем они сталкиваются с закрепленными концами и возвращаются обратно. Две волны встречаются и расходятся в разные стороны, при этом их наложение друг на друга образует стоячую волну. Струна оказывается разделенной на равные сегменты точками соприкосновения — узлами стоячей волны, при этом оставшаяся часть струны колеблется. Узлы первой, или фундаментальной частоты (ее также называют гармоникой) находятся на концах струны, для второй гармоники добавляется один узел, в середине струны, для третьей — два, делящие струну на трети, и так далее (см. рисунок).
Изображение струны
Чтобы лучше понять волновое уравнение, можно проиллюстрировать колебания струны с помощью серии фотографий. На каждой из них время останавливается, позволяя уловить профиль волны, наподобие изображенного на рисунке 1.
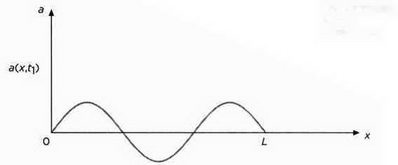
РИС. 1
Расположение струны в момент tr
Затем мы засекаем промежуток времени (ось абсцисс) и вновь отпускаем струну, концентрируя внимание на ее точке и наблюдая изменение ее положения. Изобразим это изменение, учитывая, что струна колеблется сверху вниз. Если мы расположим эти фотографии рядом, то заметим, что последовательность точек образует вторую волну (рисунок 2). Также изменение расположения точки в зависимости от времени может быть представлено таким образом, как на рисунке 3.
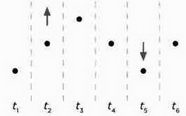
РИС. 2
Последовательность рисунков отображает изменение высоты точки струны (зафиксированное положение в момент времени x1).
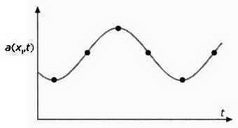
РИС. 3
Изменение положения струны, колеблющейся снизу вверх, в точке х1
Уравнение
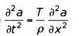
говорит нам, что скорость, с которой изменяется касательная к струне, изображенная на графике ее пространственного изменения