Все волны, вне зависимости от их размера и формы, можно описать одним математическим уравнением, точно так же, как уравнения движения частицы описываются уравнениями Ньютона. Волновая функция ψ представляет волну: она описывает ее форму в данный момент времени. На покрытой рябью поверхности пруда волновая функция указывает как велико возмущение, так называемая амплитуда волны, в данной точке x в момент времени t. Но когда Шредингер вывел волновое уравнение для волн материи де Бройля, не было понятно, что собой представляет его волновая функция. Ее можно вычислить, решив волновое уравнение для какой-то определенной физической системы, например для атома водорода. Но открытым оставался вопрос, на который Шредингер ответить затруднялся: а что именно колеблется?
В случае волн на поверхности воды или звуковых волн ответ очевиден: колеблются молекулы воды или воздуха. В XIX столетии физиков поставил в тупик свет. Считая, что необходима какая-то среда, через которую свет мог бы распространяться, им пришлось придумать таинственный “эфир”. Это продолжалось до тех пор, пока не стало понятно, что свет — это электромагнитная волна, описывающая колебания связанных электрических и магнитных полей. Шредингер верил, что волны материи столь же реальны, как и более привычные типы волн. Но что собой представляет среда, в которой распространяется электронная волна? Можно поставить вопрос иначе: что представляет собой волновая функция в уравнении Шредингера? Летом 1926 года ходила даже шутливая песенка, описывающая положение, в которое попали Шредингер и его коллеги:
Эрвин пси свою берет —
Делает любой расчет,
Но поди его спроси,
Что такое эта пси?42
В конце концов Шредингер выдвинул предположение, что волновая функция — например, электрона — тесно связана с похожим на облако распределением его электрического заряда при движении в пространстве. В волновой механике волновая функция — не та величина, которую можно измерить непосредственно. Дело в том, что она, как говорят математики, является комплексным числом. Например, число 4 + 3i состоит из двух частей: “действительной” и “мнимой”. Обычное число 4 — “действительная” часть комплексного числа 4 + 3i. Его “мнимая” часть, 3i, физического смысла не имеет, поскольку i — квадратный корень из -1. По определению, квадратный корень из числа — это другое число, которое, будучи помноженным само на себя, дает исходное. Квадратный корень из 4 равен 2, поскольку 2 х 2 = 4. Но такого числа, которое, будучи помноженным само на себя, давало бы -1, нет. Ведь и 1 х 1 = 1, и -1 х -1 = 1, так как согласно законам алгебры минус на минус дает плюс.
Волновая функция не является наблюдаемой величиной. Она представляет собой нечто неосязаемое, что измерить невозможно. Но квадрат модуля комплексного числа — это действительное число. Оно должно быть связано с чем-то, что можно измерить в лаборатории43. Так, квадрат модуля 4 + 3i равен 2544. Шредингер считал, что квадрат модуля волновой функции электрона, |ψ (x, t)|2 — это мера размазанной плотности электрического заряда в точке x в момент времени t.
Чтобы обосновать такую интерпретацию, Шредингер ввел понятие “волнового пакета”, заменяющего собой электрон. Он противился самой идее существования частиц. Он утверждал, что электрон только “кажется” похожим на частицу, но на самом деле частицей не является, хотя подавляющее число экспериментальных данных свидетельствует в пользу этого. Шредингер верил, что электрон как частица — плод воображения, а в действительности существуют только волны. Если электрон ведет себя как частица, это просто означает, что волны материи, накладываясь друг на друга, образуют волновой пакет. Двигающийся электрон — это не что иное, как волновой пакет, распространяющийся наподобие импульса, посланного слабым движением руки вдоль натянутой веревки, один конец которой мы привязали, а другой держим в руке. Чтобы волновой пакет вел себя как частица, требуется набор волн с разной длиной волны, которые, интерферируя, гасят друг друга в области пространства вне волнового пакета.
Шредингер считал, что если полный отказ от частиц и сведение всего только к волнам избавит физику от нарушений непрерывности и скачков, то это того стоит. Однако его интерпретация вскоре столкнулась с трудностями, поскольку противоречила физическому смыслу. Первый удар ей был нанесен, когда стало ясно, что если электрон — это волновой пакет, то чтобы не вступать в противоречие с экспериментами, в которых он ведет себя как частица, волны, входящие в этот пакет, должны быть размазаны по такой большой области пространства, что будут вынуждены двигаться со скоростью, превышающей скорость света.
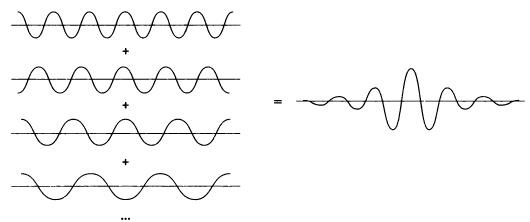
Рис. 11. Волновой пакет, образованный суперпозицией нескольких волн.
Как Шредингер ни старался, ничего поделать с таким расширением волнового пакета он не мог. Пакет состоит из волн с разными длинами и частотами. Перемещаясь в пространстве, он вскоре начинает неизбежно разбухать, поскольку составляющие его отдельные волны двигаются с разными скоростями. Чтобы волновой пакет вел себя наподобие частицы, волны должны практически мгновенно собираться вместе, быть локализованы в одной и той же точке пространства. К тому же использование волнового уравнения для гелия и других атомов приводило к тому, что представление о реальности, скрывавшееся за математическими выкладками Шредингера, исчезало. На его месте возникало абстрактное многомерное пространство, представить которое было невозможно.
В волновой функции электрона закодировано все, что надо знать об одной трехмерной волне. Однако волновую функцию двух электронов атома гелия нельзя трактовать как две трехмерные волны в обычном трехмерном пространстве. Математика показывает, что надо рассматривать одну волну, существующую в странном шестимерном пространстве. При переходе от одной клетки периодической таблицы к другой, от одного элемента к следующему число электронов возрастает на единицу. А это означает, что при каждом переходе возникает потребность в лишних трех измерениях. Если в случае лития, третьего элемента периодической таблицы, пространство должно иметь девять измерений, то уран надо снабдить пространством с 276 измерениями. Волны, распространяющиеся в таких абстрактных многомерных пространствах, не могут быть реальными физическими волнами, с помощью которых Шредингер надеялся восстановить непрерывность и избавиться от квантовых скачков.
Кроме того, интерпретация Шредингера не справлялась ни с фотоэлектрическим эффектом, ни с эффектом Комптона. Были и другие вопросы, на которые не было ответа. Как волновой пакет может обладать электрическим зарядом? Совместима ли волновая механика с квантовым спином? Если волновая функция Шредингера не является реальной волной в обычном трехмерном пространстве, то что эти волны вообще собой представляют? Ответ нашел Макс Борн.
Пятимесячное пребывание Борна в Америке подходило к концу, когда в марте 1926 года была опубликована первая статья Шредингера. Он прочитал ее по возвращении в Геттинген в апреле и, как и многие другие, почувствовал, что “захвачен врасплох”45. За время его отсутствия обстановка в квантовой физике радикально изменилась. Практически сразу Борн понял, что Шредингер построил “удивительно мощную и красивую” теорию46. Он быстро признал “превосходство математического аппарата волновой механики”, поскольку она позволяет сравнительно легко справиться с “фундаментальной задачей атомной физики” — вычислением спектра атома водорода47. Чтобы применить матричную теорию к атому водорода, потребовался человек такого таланта, как Паули. Может быть, Борн и оказался захвачен врасплох, но с волнами материи он был знаком уже давно — задолго до того, как Шредингер опубликовал свою работу.



