К великому восторгу Фейнмана, у Карла рано проявились способности к науке. Когда сыну было двенадцать, Фейнман показал ему необычную фотографию, которую привез из канадской лаборатории, и Карл верно догадался, что на ней изображен «рисунок рассеяния лазерного луча через решетку со стандартно расположенными квадратными отверстиями». Фейнман тут же стал хвастаться друзьям: «Я готов был его убить! А ведь я боялся спрашивать, какое фокусное расстояние объектива он использует». Он пытался не наседать и убеждал себя: какую бы стезю ни избрали его дети, он будет рад («Хочешь, играй на трубе, будь социальным работником, да хоть марки собирай», — писал он Карлу.) Главное, чтобы они были счастливы и успешны в своей профессии. Но когда Карл окончил колледж и поступил в университет, а это был МТИ, его выбор, пожалуй, был единственным, который гарантированно мог выбить отца из колеи. «Что ж, — писал Фейнман, — я долго пытался понять и наконец, как мне кажется, смирился с твоим решением стать философом». Но на самом деле не смирился. Подобно бизнесмену, чей сын захотел стать поэтом, он чувствовал, что его предали и обманули.
«Я все время думаю: как можно быть хорошим философом? Видимо, как сын богача, который ни разу не задумывался о деньгах и решает стать поэтом (потому что ждет, что его старик заплатит за все), ты предпочел философию рациональной мысли (потому что твой старик продолжит рационально мыслить за всех). Зато теперь ты сможешь подняться над здравым смыслом и воспарить к гораздо более высоким и тонким аспектам интеллекта».
«И, наверное, здорово, — саркастически добавлял он, — что у тебя это получается». Воспитание детей заставило его задуматься о системе образования и уроках, которые преподал ему собственный отец. Когда Карлу исполнилось четыре, Фейнман активно выступал против нового учебника естественных наук для первого класса, который собирались ввести в калифорнийских школах. На первой странице были изображены: заводная игрушечная собака, настоящая собака и мотоцикл. Под картинками значился вопрос: «Что заставляет их двигаться?» Фейнман пришел в ярость, узнав предполагаемый ответ — «энергия».
Это тавтология, утверждал он, определение, лишенное смысла. Фейнман, посвятивший всю свою карьеру попыткам постичь глубокий абстрактный смысл энергии, был убежден, что в начале обучения естественным наукам лучше взять и разобрать эту самую игрушечную собачку, обнажив скрытый хитроумный механизм шестеренок и храповиков. Сказать первокласснику, что «собачкой движет энергия» — все равно что заявить «ею движет Бог» или «ею движет способность двигаться». Он предложил простой тест, с помощью которого можно было бы выявить, чему учит педагог — мыслить или запоминать пустые определения:
«Надо дать ученикам задание: не используя слово “энергия”, самостоятельно рассказать, что нового они узнали о движении собачки».
Другие стандартные объяснения из учебника были такими же неинформативными: «объекты падают из-за гравитации»; «объекты изнашиваются из-за трения». Фейнман преподавал фундаментальные основы первокурсникам Калтеха, но считал, что все то же самое доступно пониманию первоклассника. «Подошва ботинок изнашивается, потому что трется о тротуар; она зацепляется за маленькие неровности и бугорки на дороге и рвется». Вот это настоящие знания, считал он. «А если просто сказать “ботинки изнашиваются из-за трения”, это не наука, и меня такие формулировки удручают».
За время работы в Калтехе Фейнман прочел тридцать четыре программных курса — примерно по одному в год. Большинство из них предназначались аспирантам и были специальными: «Продвинутый курс квантовой механики»; «Вопросы теоретической физики». Тема курса часто совпадала с текущими научными интересами Фейнмана. Порой, сами того не осознавая, слушатели становились свидетелями первого и последнего отчета о значительном открытии, которое любой другой физик тут же поспешил бы опубликовать. А еще он почти двадцать лет читал курс, не упомянутый ни в одном списке, — «Физика Х». Раз в неделю аспиранты собирались и задавали любые научные вопросы, какие только пожелают, а Фейнман отвечал, и это была полная импровизация. Он производил на студентов неизгладимое впечатление: те часто уходили из лаборатории Лауритцена в подвале Калтеха с ощущением, что посетили сеанс всеведущего оракула, который, однако, нисколько не кичился своим знанием, а считал его доступным всем и каждому. В то время как предмет его изучения — квантовые частицы — становился все более абстрактным и эзотерическим, он верил, что истинное понимание требует ясности. Один физик как-то попросил его в простых терминах объяснить стандартное явление: почему частицы с дробным спином подчиняются статистике Ферми — Дирака. Фейнман пообещал подготовить лекцию для первокурсников по этой теме. И в кои-то веки у него ничего не вышло. «Я не смог упростить эту концепцию до уровня новичков, — признался он через несколько дней и добавил: — Значит, на самом деле мы ее не понимаем»
[167].
Участвуя в образовательных инициативах, он думал прежде всего о своих детях. В 1964 году он принял редкое для ученого такого уровня решение вступить в общественный комитет, который занимался отбором учебников для калифорнийских начальных школ. Исторически членство в этом комитете было синекурой; участники негласно получали «пряники» от издателей. Как выяснил Фейнман, учебники почти никто не читал. Но он вознамерился прочесть их все — и тонны книг доставили к нему домой. Это была эпоха «новой математики» в начальном образовании — попытка модернизировать преподавание в школе путем введения таких сложных концепций, как теория множеств и недесятичное исчисление. Новая математика закрепилась в школах страны на удивление быстро, несмотря на беспокойство родителей, которое хорошо передавала карикатура в журнале New Yorker. «Смотри, пап, — говорила маленькая девочка, — это множество включает все заработанные тобой доллары; твои расходы — подмножество. А твои налоговые вычеты — подмножество этого подмножества».
Фейнман модернизаторов не поддержал. Вместо этого он проткнул мыльный пузырь новой математики. Своим коллегам по комитету он заявил, что множества в этих учебниках не что иное, как извращенный педантизм, введение новых определений ради самих определений, типичный пример обучения словам без объяснения понятий. Например, первоклассникам предлагали решить задачу: «Определи, равно ли множество конфет множеству девочек». Фейнман считал это настоящей болезнью. Из формулировки просто убрали всю ясность, сделав ее более размытой по сравнению с обычным предложением: «Определи, хватит ли девочкам конфет». Специальная терминология может подождать своего часа, говорил он, а уж специфический язык теории множеств вообще никогда никому не пригодится. Зато, как обнаружилось, в модернизированных учебниках не затрагивались те сферы, в которых эта теория становится действительно полезной и имеет смысл, а не остается пустым определением, в частности различные степени бесконечности.
«Это крайний пример употребления новых слов и определений, так как факты здесь вообще не объясняются… Большинство людей, прочитавших этот учебник, наверняка удивятся, если я скажу им, что символы
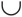 или
или
 , обозначающие сумму и пересечение множеств… и все сложные обозначения множеств, которые в нем содержатся, почти никогда не встречаются в работах по теоретической физике, в инженерии, бизнесе, арифметике, компьютерном дизайне и прочих сферах, где используется математика».
, обозначающие сумму и пересечение множеств… и все сложные обозначения множеств, которые в нем содержатся, почти никогда не встречаются в работах по теоретической физике, в инженерии, бизнесе, арифметике, компьютерном дизайне и прочих сферах, где используется математика».



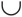 или
или
 , обозначающие сумму и пересечение множеств… и все сложные обозначения множеств, которые в нем содержатся, почти никогда не встречаются в работах по теоретической физике, в инженерии, бизнесе, арифметике, компьютерном дизайне и прочих сферах, где используется математика».
, обозначающие сумму и пересечение множеств… и все сложные обозначения множеств, которые в нем содержатся, почти никогда не встречаются в работах по теоретической физике, в инженерии, бизнесе, арифметике, компьютерном дизайне и прочих сферах, где используется математика».