Никакого поля. Никакого самосогласованного действия. Следуя утверждению Фейнмана, законы природы были не столько открыты учеными, сколько умозрительно выведены. Впрочем, их смысл, переведенный на язык слов, несколько размывался. Фейнмана интересовал не столько сам факт воздействия электрона на самого себя, сколько возможность обоснованно отбросить эту концепцию. То есть не существование поля в природе, а возможность его существования в уме физика. Когда Эйнштейн провозгласил, что эфира не существует, он говорил, что отсутствует что-то реальное, или, по крайней мере, то, что должно было существовать, — представьте хирурга, который вскрыл грудную клетку и не обнаружил там пульсирующего сердца. С полем все было иначе. Оно было придумано, а не существовало в реальности. Английские ученые Майкл Фарадей и Джеймс Максвелл, которые ввели это понятие в XIX веке, полагая, что оно столь же необходимо, как хирургический скальпель, начали чуть ли не извиняться. Они не ожидали, что их слова воспримут буквально, когда писали о «силовых линиях», которые Фарадей наблюдал, разбрасывая металлические опилки вблизи магнита, или о «промежуточных шестернях»
[83], псевдомеханических невидимых вихрях, которые, по представлениям Максвелла, заполняли пространство. Они заверяли своих читателей, что это были всего лишь аналогии, хотя и обоснованные математически.
Понятие поля было предложено не просто так. Оно давало возможность свести воедино свет и электромагнетизм и было не чем иным, как преобразованием одного в другое. Как и абстрактный приемник ныне не существующего эфира, поле идеально объясняло распространение волн, а энергия, казалось, действительно волнообразно пульсировала из его источников. Каждый экспериментатор, так же увлеченно изучающий электрические цепи и магниты, как Фарадей и Максвелл, мог почувствовать, как «вибрации» или «волновые движения» движутся циклически, подобно кручению колеса
[84]. Но главное, поле позволяло объяснить, почему находящиеся на расстоянии объекты взаимодействуют друг с другом. В поле силы распространялись непрерывно, от одного места к другому. Никаких скачков, никакого волшебного подчинения непонятно откуда поступающим командам. Американский физик и философ Перси Бриджмен сказал: «Гораздо проще принять рациональный взгляд на то, что гравитация Солнца действует на Землю сквозь пространство, чем верить, что воздействующая сила «перескакивает» через разделяющее их расстояние и находит цель благодаря своей телеологической проницательности». К тому времени ученые уже забыли, что поле само по себе тоже несло налет магии: волнообразное нечто, которого не было, и пустое пространство, не вполне пустое и, строго говоря, не совсем пространство. Или, как позже сказал теоретик Стивен Вайнберг, «напряжение в мембране, но без самой мембраны». Понятие поля стало настолько привычным для физиков, что даже материя порой казалась им неким придатком, «точкой» этого поля, «пятном», или, как сказал Эйнштейн, тем местом, где поле было особенно интенсивно.
Принимать гипотезу поля или отрицать ее — так или иначе, к 1930 году это был уже вопрос метода, а не реальности. События 1926–1927 годов многое прояснили. Никто уже не был так наивен, чтобы сомневаться в существовании матриц Гейзенберга или волновых уравнений Шрёдингера. Это два разных взгляда на одни и те же процессы. В поисках новой теории Фейнман обратился к классическим представлениям о взаимодействии частиц. Ему пришлось столкнуться с волнообразным распространением энергии и обманчивым действием на расстоянии. В то же время Уилера заинтересовала абсолютно четкая концепция того, что электроны могут взаимодействовать напрямую, без участия поля.
Сгибы и ритмы
Во время учебы в аспирантуре Фейнману приходилось чаще общаться с математиками, чем с физиками. Студенты, обучающиеся на двух потоках, собирались каждый полдень в общем холле на чай — опять же, дань английским традициям, — и Фейнман постоянно слышал разговоры математиков на совершенно чуждом ему профессиональном языке. Математика уже переставала развиваться как наука, непосредственно используемая в современной физике, а сами математики все больше и больше склонялись к изучению таких кажущихся непонятными разделов как, например, топология
[85], рассматривающая фигуры в двух-, трех- и многомерных пространствах без учета фиксированных длин или углов. Будущие математики и физики все заметнее отдалялись друг от друга. В последний год обучения их практически ничего не связывало — ни совместные курсы, ни темы для разговоров. Фейнман же во время общих чаепитий, присоединившись к одной из групп или сидя на диване, слушал, что говорили математики о доказательствах. Так или иначе, он интуитивно чувствовал, какая теорема может быть выведена из какой леммы, даже если не понимал толком предмета спора. Ему нравились эти странные беседы. Нравилось угадывать противоречащие логике ответы на не поддающиеся наглядному представлению вопросы. Нравилось, как и всем физикам, подкалывать присутствующих, утверждая, что математики все время пытаются доказать очевидное. И хотя он подшучивал над ними, его восхищало это общество людей, увлеченных непостижимой наукой. Одним из друзей Ричарда был Артур Стоун, терпеливый молодой англичанин, обучавшийся в Принстоне на стипендию. Другим — Джон Тьюки, впоследствии ставший одним из известных в мире статистиков. Эти парни очень серьезно относились к своему свободному времени. Стоун привез из Англии блокноты, в которые можно было вставлять листы, а так как стандартная американская бумага была шире его блокнотов на два с половиной сантиметра, то у него всегда имелся большой запас бумажных полосок, из которых получались разные фигурки. Он попробовал сгибать бумагу по диагонали под углом 60° и получил ряд равносторонних треугольников. А затем, по этим сгибам, он сложил полоски в идеальный шестигранник.
Согнув полоску так, что ее края соединились, он обнаружил, что придумал необычную игрушку. Он зажал противоположные углы шестигранника и получил странную фигуру, напоминающую оригами, — новый шестигранник с другим набором треугольников. При повторном сжатии открывались другие грани. Еще один «флекс»
[86] — и фигура принимала изначальный вид. В итоге получалась плоская фигурка, которую можно было выворачивать туда-сюда.
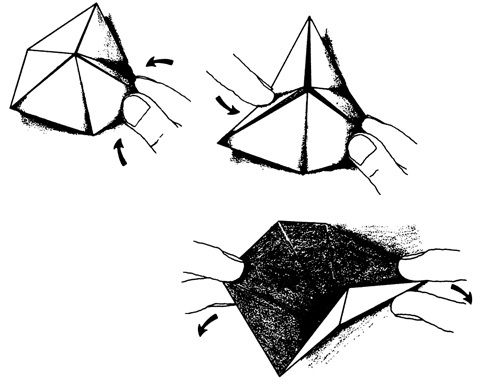
Как сделать гексафлексагон
Стоун занимался этим всю ночь, а утром взял длинную полоску и подтвердил возникшую у него гипотезу: более сложный шестигранник мог бы состоять не из трех, а из шести различных поверхностей. На этот раз цикл процесса изготовления оказался не таким простым. Три грани появлялись снова и снова, в то время как остальные три были скрыты. Нетривиальный вызов его топологическому воображению. Искусство оригами развивалось столетиями, но никому прежде не удавалось воспроизвести столь изящную фигуру. В течение нескольких дней такие флексагоны, в дальнейшем получившие названия гексафлексагоны (шесть сторон, шесть поверхностей), циркулировали по обеденному залу во время обедов и ужинов. А затем появилась Комиссия по изучению флексагонов, в состав которой вошли Стоун, Тьюки, математик Брайант Такерман и их друг физик Фейнман. Оттачивая свое мастерство и ловкость в обращении с листами и полосками бумаги, они сделали гексафлексагоны с двенадцатью поверхностями, скрытыми внутри, потом с двадцатью четырьмя и даже с сорока восьмью. Количество вариаций в каждом виде флексагонов стремительно увеличивалось в соответствии с далеко не очевидным законом. Теория флексагонов развивалась, занимая свое место на стыке топологии и теории сетей. Фейнман же внес в нее свой вклад, придумав диаграмму, впоследствии названную в его честь, которая показывала все возможные конфигурации гексафлексагона.



