Фейнман и Дирак встретились снова через много лет. Они обменялись парой неловких фраз, но их разговор был столь примечателен, что оказавшийся рядом физик немедленно записал подслушанный диалог, прозвучавший как отрывок из театральной постановки.
— Я Фейнман.
— Я Дирак. (Молчание.)
— Наверное, здорово быть человеком, который открыл то уравнение.
— Это было много лет назад. (Пауза.) Над чем работаете?
— Над мезонами.
— Высчитываете уравнение?
— Это очень сложно.
— Нужно стараться.
Дирак совершил нечто важное, до него никто этого не делал: благодаря ему само открытие уравнения стало считаться чем-то, достойным восхищения. Для физиков же уравнение Дирака имело и всегда будет иметь одно волшебное свойство, схожее с появлением кролика из шляпы. Оно было релятивистским: его не нужно было искусственно адаптировать для околосветовых скоростей. Уравнением также было установлено, что спин является естественным свойством электрона. Осознание этого факта приближало к пониманию обманчивости представлений о том, что новый язык физики далек от реальности. Спин не был настолько странным и абстрактным явлением, как другие свойства частиц, открытые позднее. Даже названия этих других свойств — цвет и аромат частицы — были отчаянной, пусть и остроумной попыткой указать на их нереальность
[122]. Спин, хоть и с трудом, но можно было представить, рассматривая электрон как маленькую луну: тогда спин можно ассоциировать с вращением электрона вокруг собственной оси. Но если электрон — бесконечно малая частица, он вряд ли мог вращаться в общепринятом смысле этого слова. Электрон — это и волна вероятности, и волна, которая отражается от стен ограничивающей камеры; как могут эти объекты вращаться? Каким образом спин возможно измерить в целых или дробных числах
[123] (как в квантовой механике)? Физики стали считать спин не вращением, а своего рода симметрией, способом математически подтвердить, что система может совершать определенные вращательные движения.
Спин был проблемным местом теории Фейнмана, описанной в его принстонской диссертации. В обычной механике величина действия не обладала таким свойством. Его теория оказалась бы бесполезной, если бы ее нельзя было применить к вращающемуся релятивистскому электрону Дирака. Среди препятствий, мешающих ему продвинуться дальше, проблема спина была главной. Неудивительно, что он повсюду замечал вращающиеся предметы — как ту тарелку в столовой с колебанием по траектории в долю секунды. Следующий шаг был характерным для Фейнмана: он свел проблему к схеме, к одномерной вселенной (или двухмерной, с пространством и временем). И в этой линейной вселенной частица могла иметь только одну траекторию движения — вперед и назад. Она носилась в двух противоположных направлениях, как безумный жук. Цель Фейнмана состояла в том, чтобы, начав с метода, открытого им еще в Принстоне, — суммирования всех возможных траекторий движения одной частицы, — выяснить, удастся ли ему вывести одномерное уравнение Дирака в этом одномерном мире. Вот что он написал:
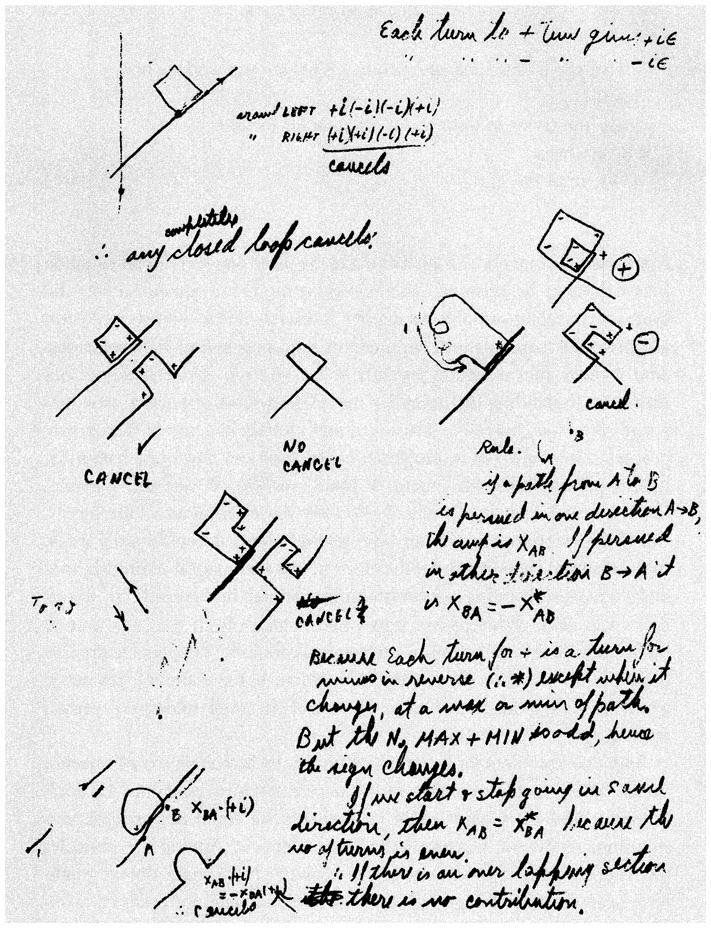
Фейнман рассматривал траекторию, которую описывает частица в одномерной вселенной, то есть в условиях, где она вынуждена двигаться только вперед и назад и всегда со скоростью света. Он представил это движение в виде диаграммы, отметив на горизонтальной оси изменение пространства, а на вертикальной — изменение времени; течение времени изображалось как движение вверх. При помощи этой модели он выяснил, что может вывести центральное уравнение квантовой механики, сложив все траектории, которые имеет одна частица.
Геометрия уравнения Дирака. Первый аспект
Вероятность = квадрат суммы движений по каждой траектории.
Зигзагообразная траектория, частицы движутся со скоростью света.
Он добавил кое-что еще — простейшую схему подсчета этих зигзагов. Горизонтальная ось соответствовала измерениям в пространстве, вертикальная отображала время. Таким образом, у Фейнмана начала выстраиваться теория, применимая к одномерному пространству. Спин частиц подразумевал наличие фазы, подобной фазе волны, и Фейнман выдвинул несколько предположений (лишь отчасти произвольных) о том, что будет происходить с фазой каждый раз, когда частица делает зигзаг. Фаза была ключевым фактором в расчете суммы траекторий, потому что траектории либо компенсировали, либо усиливали друг друга в зависимости от наложения фаз (интерферировали). Фейнман не предпринимал попыток опубликовать этот фрагмент теории, хотя его обрадовал прогресс в расчетах. Теперь перед ним стояла задача применить эту теорию к пространству, имеющему более одного измерения, — иными словами, попытаться «развернуть» пространство. Но это у него пока не получалось, хоть он и проводил долгие часы в библиотеке, в кои-то веки штудируя старые математические труды.
Уменьшая бесконечность
Состояние фрустрации, которое испытывал Фейнман в первые послевоенные годы, отражало общее настроение, царившее в среде именитых физиков-теоретиков. Это было растущее чувство беспомощности, ощущение, что они потерпели поражение. Поначалу об этих настроениях не говорили открыто, потом ими стали делиться, но в пределах узкого сообщества. Публичная слава физиков никогда еще не была столь велика; остальное же оставалось невидимым миру.
Обычному человеку сложно понять причину этого состояния. Дело в том, что в своих расчетах ученые столкнулись с одной сложностью. По мере решения уравнения некоторые последовательные величины расходились, то есть увеличивались, хотя должны были уменьшаться по мере вычисления. Например, вычисление каждой новой цифры после запятой в массе электрона приводило к бесконечным величинам. С точки зрения физики казалось, что по мере приближения к электрону его заряд и масса увеличиваются. Но в результате ученые сталкивались с бесконечностями, с которыми Фейнман бился с самого Принстона. То есть квантовая механика позволяла вычислить уравнение в первом приближении, но дальше следовал сизифов труд. Чем больше физики старались повысить точность, тем менее точными становились их расчеты. Такие величины, как масса электрона, становились бесконечными (если теорию применяли к предельной массе). Сложно понять ужас, который испытали ученые; в популярных научных обзорах того периода об этом ничего не говорилось. Но тупик подстерегал физиков не только в теории; вскоре они столкнулись с проблемами и в практических расчетах. «Полагая, что знаю геометрию, — рассказывал Фейнман позднее, — я пытался высчитать диагональ квадрата со стороной 2,25 м. Но выяснилось, что не такой уж я эксперт, потому что в результате моих расчетов получалась бесконечность. Все было бессмысленно».



