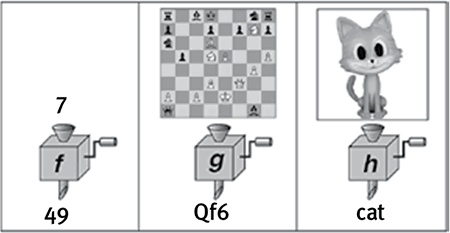
Рис. 2.5
Каждое вычисление использует информацию на входе, чтобы преобразовывать ее, выполняя над ней то, что математики называют функцией. У функции f (слева) на входе последовательность бит, представляющих число; в результате вычислений она дает на выходе его квадрат. У функции g (в центре) на входе последовательность бит, представляющих позицию на шахматной доске; в результате вычислений она дает на выходе лучший ход для белых. У функции h (справа) на входе последовательность бит, представляющих изображение, в результате вычислений она дает на выходе соответствующую текстовую подпись.
Другими словами, если вы можете вычислять достаточно сложные функции, то вы сумеете построить машину, которая будет весьма «умной» и сможет достигать сложных целей. Таким образом, нам удается внести несколько большую ясность в вопрос о том, как может материя быть разумной, а именно: как могут фрагменты бездумной материи вычислять сложные функции.
Речь теперь идет не о неизменности надписи на поверхности золотого кольца и не о других статических запоминающих устройствах — интересующее нас состояние должно быть динамическим, оно должно меняться весьма сложным (и, хорошо бы, управляемым/программируемым) образом, переходя от настоящего к будущему. Расположение атомов должно быть менее упорядоченным, чем в твердом и жестком теле, где ничего интересного не происходит, но и не таким хаотичным, как в жидкости или в газе. Говоря точнее, мы бы хотели, чтобы наша система восприняла начальные условия задачи как свое исходное состояние, а потом, предоставленная самой себе, как-то эволюционировала, и ее конечное состояние мы бы могли рассматривать как решение данной ей задачи. В таком случае мы можем сказать, что система вычисляет нашу функцию.
В качестве первого примера этой идеи давайте построим из нашей неразумной материи очень простую (но от этого не менее важную) систему, вычисляющую функцию NAND
[12] и потому получившую название гейт NAND
[13]. У нее на входе два бита, а на выходе один: это 0, если оба бита на входе 1, во всех остальных случая — это 1. Если в одну сеть с батареей и электромагнитом мы вставим два замыкающих сеть ключа, то электромагнит сработает тогда, и только тогда, когда оба ключа замкнуты (находятся в состоянии «on»). Давайте поместим под ним еще один ключ, как показано на рис. 2.6, так что магнит, срабатывая, всякий раз будет размыкать его. Если мы интерпретируем первые два ключа как два бита на входе, а третий — как бит на выходе, то мы и получим то, что назвали гейтом NAND: третий ключ будет разомкнут только тогда, когда первые два замкнуты. Есть очень много более практичных способов сделать гейт NAND — например, с помощью транзисторов, как показано на рис. 2.6. В нынешних компьютерах гейты NAND чаще всего встроены в микросхемы или иные компоненты, выращенные из кристаллов кремния.
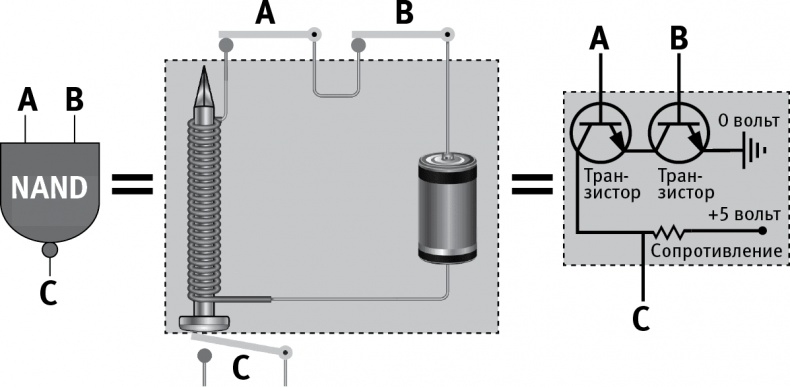
Рис. 2.6
Логический вентиль (гейт) NAND по заданным на входе двум битам А и В вычисляет третий бит С в соответствии с правилом: C = 0, если A = B = 1, и C = 0 в любом другом случае, — и посылает его на выход. В качестве гейта NAND можно использовать много различных физических устройств. В электрической цепи на средней части рисунка ключи А и В соответствуют битам на входе со значениями 0 при размыкании и 1 при замыкании. Когда они оба замкнуты, идущий через электромагнит ток размыкает ключ С. На схеме в правой части рисунка битам соответствуют значения потенциалов — 0, когда потенциал равен нулю, и 1, когда потенциал равен 5 вольтам. При подаче напряжения на базы обоих транзисторов (А и В) потенциал в точке С падает практически до нуля.
В информатике есть замечательная теорема, которая утверждает, что гейт NAND универсален: то есть вычисление любой вполне определенной функции
[14] может быть осуществлено гейтами NAND, соединенными друг с другом. Так что если у вас есть достаточное количество гейтов NAND, вы можете собрать из них устройство, вычисляющее все что угодно! На случай, если у вас возникло желание посмотреть, как это работает, у меня есть схема (рис. 2.7), на которой вы увидите, как умножаются числа при помощи одних только гейтов NAND.
Исследователи из MIT Норман Марголус и Томмазо Тоффоли придумали слово «computronium» (компьютрониум), обозначающее любую субстанцию, которая может выполнять любые вычисления. Мы только что убедились, что создать компьютрониум не так уж и сложно: эта субстанция всего лишь должна быть способна соединять гейты NAND друг с другом любым желаемым способом. Разумеется, существуют и мириады других компьютрониумов. Например, еще один легко создать из предыдущего, заменив все гейты NAND на NOR: у него на выходе будет 1 только тогда, когда на оба входа подается 0. В следующем разделе мы обсудим нейронные сети, которые также способны выполнять произвольные вычисления, то есть и они ведут себя как компьютрониум. Ученый и предприниматель Стивен Вольфрам показал, что то же может быть сказано о простых устройствах, получивших название клеточных автоматов, которые периодически подправляют каждый бит в зависимости от того, в каком состоянии находятся биты по соседству. А еще в 1936 году Алан Тьюринг доказал в своей ставшей ключевой статье, что простая вычислительная машина (известная сейчас как «универсальный компьютер Тьюринга»), способная оперировать некоторыми символами на бумажной ленте по некоторым правилам, также способна выполнять любые вычисления. Одним словом, материя не просто обладает способностью к любым вполне определенным вычислениям, но и может производить их самыми разнообразными способами.
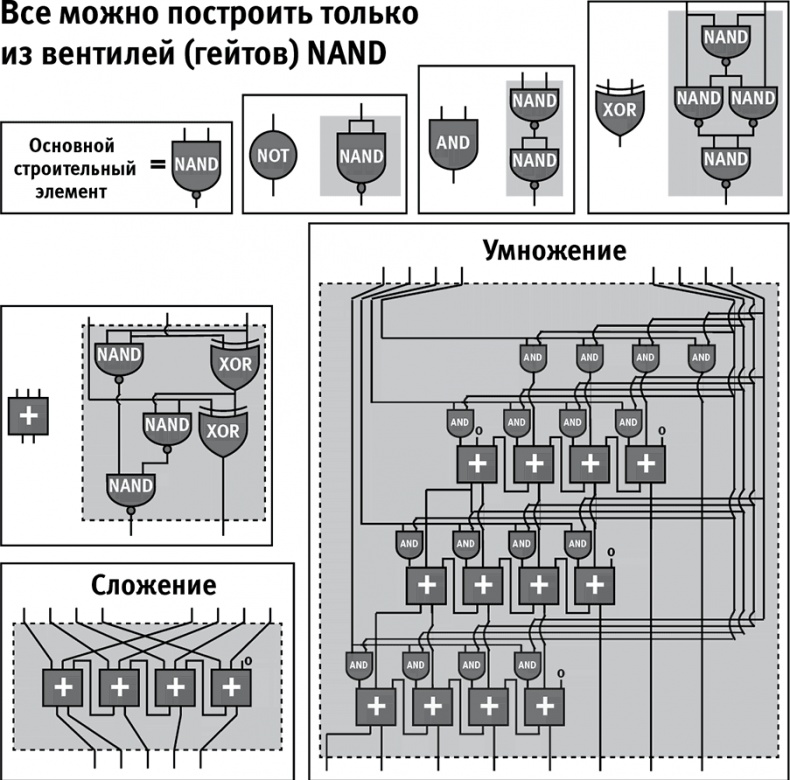
Рис. 2.7





