Рис. 2.10
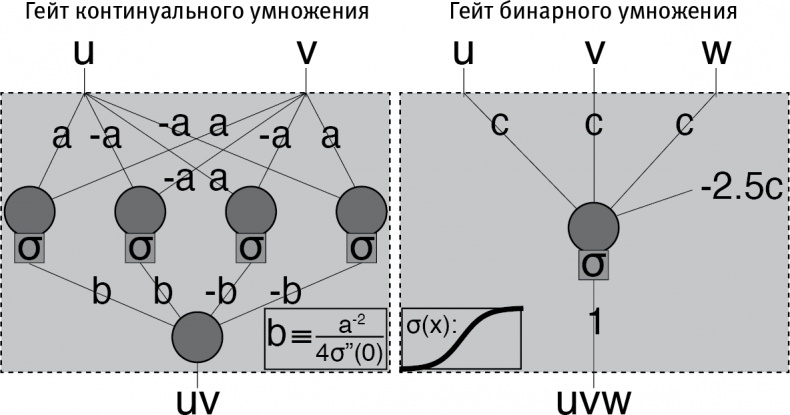
Вещество может производить умножение, используя не гейты NAND, как на рис. 2.7, а нейроны. Для понимания ключевого момента здесь не требуется вникать в детали, достаточно только отдавать себе отчет, что нейроны (как биологические, так и искусственные) не только способны производить математические действия, но их для этого требуется значительно меньше, чем гейтов NAND. Вот еще факультативные детали для упертых фанатов математики: кружочками обозначено сложение, квадратики обозначают применение функции σ, а прямые отрезки — умножение на число, которое этот отрезок пересекает. На входе — вещественное число (слева) или бит (справа). Умножение становится сколь угодно точным при а → 0 (слева) и при с → ∞ (справа). Левая сеть работает при любой функции σ(х), имеющей изгиб в нуле σ»(0) ≠ 0), что можно доказать разложением функции σ(х) по формуле Тейлора. Для сети справа надо, чтобы функция σ(х) стремилась к нулю и к единице при очень малых и очень больших х соответственно, так чтобы соблюдалось условие uvw = 1, только когда u + v + w = 3. (Эти примеры взяты из статьи моего студента Генри Лина: https://arxiv.org/abs/1608.08225, проверена 18 мая 2018.) Комбинируя умножения и сложения, можно вычислять любые полиномы, с помощью которых, как известно, мы можем получить апроксимацию любой гладкой функции.
Впервые услышав об этом, я был озадачен: как что-то до такой степени простое может вычислить нечто произвольно сложное? Например, как вы сможете даже просто-напросто что-то перемножать, когда вам разрешено только вычислять взвешенные средние значения и применять одну фиксированную функцию? Если вам захочется проверить, как это работает, на рис. 2.10 показано, как всего пять нейронов могут перемножать два произвольных числа и как один нейрон может перемножить три бита.
Хотя вы можете доказать теоретическую возможность вычисления чего-либо произвольно большой нейронной сетью, ваше доказательство ничего не говорит о том, можно ли это сделать на практике, располагая сетью разумного размера. На самом деле, чем больше я об этом думал, тем больше меня удивляло, что нейронные сети и в самом деле так хорошо работали.
Предположим, что у вас есть черно-белые мегапиксельные фотографии, и вам их надо разложить в две стопки — например, отделив кошек от собак. Если каждый из миллиона пикселей может принимать одно из, скажем, 256 значений, то общее количество возможных изображений равно 2561000000, и для каждого из них мы хотим вычислить вероятность того, что на нем кошка. Это означает, что произвольная функция, которая устанавливает соответствие между фотографиями и вероятностями, определяется списком из 2561000000 позиций, то есть числом большим, чем атомов в нашей Вселенной (около 1078). Тем не менее нейронные сети всего лишь с тысячами или миллионами параметров каким-то образом справляются с такими классификациями довольно хорошо. Как успешные нейронные сети могут быть «дешевыми» в том смысле, что от них требуется так мало параметров? В конце концов, вы можете доказать, что нейронная сеть, достаточно маленькая для того, чтобы вписаться в нашу Вселенную, потерпит грандиозное фиаско в попытке аппроксимировать почти все функции, преуспев лишь в смехотворно крошечной части всех вычислительных задач, решения которых вы могли бы от нее ждать.
Я получил огромное удовольствие, разбираясь с этой и другими, связанными с ней, загадками вместе со студентом по имени Генри Лин. Среди разнообразных причин испытывать благодарность к своей судьбе — возможность сотрудничать с удивительными студентами, и Генри — один из них. Когда он впервые зашел в мой офис и спросил, хотел бы я поработать с ним, я подумал, что, скорее, мне надо было бы задавать такой вопрос: этот скромный, приветливый юноша с сияющими глазами из крошечного городка Шревепорт в штате Луизиана уже успел опубликовать восемь научных статей, получить премию Forbes 30-Under-30 и записать лекцию на канале TED, получившую более миллиона просмотров — и это всего-то в двадцать лет! Год спустя мы вместе написали статью, в которой пришли к удивительному заключению: вопрос, почему нейронные сети работают так хорошо, не может быть решен только методами математики, потому что значительная часть этого решения относится к физике.
Мы обнаружили, что класс функций, с которыми нас познакомили законы физики и которые, собственно, и заставили нас заинтересоваться вычислениями, — это удивительно узкий класс функций, потому что по причинам, которые мы все еще не полностью понимаем, законы физики удивительно просты. Более того, крошечная часть функций, которую могут вычислить нейронные сети, очень похожа на ту крошечную часть, интересоваться которыми нас заставляет физика! Мы также продолжили предыдущую работу, показывающую, что нейронные сети глубокого обучения (слово «глубокое» здесь подразумевает, что они содержат много слоев) гораздо эффективнее, чем мелкие, для многих из этих функций, представляющих интерес. Например, вместе с еще одним удивительным студентом MIT, Дэвидом Ролником, мы показали, что простая задача перемножения n чисел требует колоссальных 2n нейронов для сети с одним слоем и всего лишь около 4n нейронов в глубокой сети. Это помогает объяснить не только возросший энтузиазм среди исследователей AI по отношению к нейронным сетям, но также и то, зачем эволюции понадобились нейронные сети у нас в мозгу: если мозг, способный предвидеть будущее, дает эволюционное преимущество, в нем должна развиваться вычислительная архитектура, пригодная для решения именно тех вычислительных задач, которые возникают в физическом мире.
Теперь, когда мы знаем, как нейронные сети работают и как вычисляют, давайте вернемся к вопросу о том, как они могут учиться. В частности, как может нейронная сеть улучшать свои вычислительные способности, обновляя состояние своих синапсов.
Канадский психолог Дональд Хебб в своей книге 1949 года The Organization of Behavior, вызвавшей живой отклик, утверждал, что если бы два соседних нейрона часто оказывались активны («светились») одновременно, то их синаптическая связь усиливалась бы, обучая их включать друг друга — эта идея нашла отражение в популярной присказке «Связаны вместе, светятся вместе». Хотя до понимания в подробностях, как именно происходит обучение в настоящем мозгу, нам еще далеко, и исследования показывают, что ответы во многих случаях должны будут далеко выходить за рамки простых предложенных правил вроде того, что стало известно как «обучение по Хеббу», даже эти простые правила, тем не менее, способны объяснить, каким образом происходит обучение нейронных сетей во многих интересных случаях. Джон Хопфилд ссылался на обучение по Хеббу, которое позволило его исключительно простой искусственной нейронной сети сохранить много сложных воспоминаний путем простого повторения. Такое экспонирование информации в целях обучения обычно называют «тренировкой», когда речь идет об искусственных нейронных сетях (а также о животных или о людях, которым надо приобрести определенный навык), хотя слова «опыт», «воспитание» или «образование» тоже подходят. В искусственных нейронных сетях, лежащих в основе современных систем AI, обучение по Хеббу заменено, как правило, более сложными правилами с менее благозвучными названиями, такими как обратное распространение ошибки (backpropagation) или спуск по стохастическому градиенту (stochastic gradient descent), но основная идея одна и та же: существует некоторое простое детерминированное правило, похожее на закон физики, с помощью которого синапсы со временем обновляются. Словно по волшебству, пользуясь этим простым правилом, нейронную сеть можно научить чрезвычайно сложным вычислениям, если задействовать при обучении большие объемы данных. Мы пока еще не знаем точно, какие правила использует при обучении наш мозг, но, каков бы ни был ответ, нет никаких признаков, что эти правила нарушают законы физики.



