У Алисы на борту есть маленький космический челнок. Она собирается отчалить в нем от своего звездолета, уменьшить немного скорость своего кругового движения, тормозя двигателем челнока, а потом выключить двигатель и перейти в свободный полет. Боб обещает ей оставаться в своем звездолете и понаблюдать за ней. Чтобы помочь Бобу в его наблюдениях, Алиса прикрепляет к своему челноку ярко-желтую мигалку, которая вспыхивает раз в секунду.
По замыслу их эксперимента, как только тормозной двигатель челнока Алисы будет выключен, она начнет двигаться по геодезической в рамках геометрии шварцшильдовской черной дыры. Раз ее начальная скорость будет меньше, чем скорость ее звездолета на круговой орбите, челнок перейдет на новую орбиту, которая, конечно, будет несколько ближе к черной дыре. Если Алиса будет держать тормозной двигатель челнока включенным до полной остановки своего обращения, то она спикирует на черную дыру в радиальном направлении и будет проглочена горизонтом событий. Алиса, конечно, девушка безбашенная, но все же такой сценарий ей не нравится: она собирается сохранить определенную угловую скорость, которая позволила бы ей в этом падении лихо промчаться мимо черной дыры, обогнуть ее и снова попасть на первоначальную орбиту. Оказавшись там, она может вернуться на свой корабль или снова и снова повторять тот же головокружительный трюк с торможением.
Но вот что она должна иметь в виду: орбита ее челнока будет очень сильно прецессировать, и чем глубже в направлении черной дыры она нырнет, тем сильнее будет прецессия. Даже при небольшой эллиптичности прецессия ее орбиты будет гораздо больше, чем у орбиты Меркурия при его обращении вокруг Солнца, так как в абсолютных единицах тяготение черной дыры, у которой находятся Алиса и Боб, гораздо сильнее, чем где бы то ни было в Солнечной системе. Но, несмотря на это отличие, эффекты прецессии, которые могут наблюдать Алиса и Боб, описываются вычислениями, очень похожими на те, что проделал Эйнштейн для объяснения особенностей орбиты Меркурия.
Поэкспериментировав с разными орбитами, Алиса наконец обнаруживает, что может заставить свою орбиту прецессировать настолько, насколько захочет. Вот как она это сделает: отчалив от своего звездолета, будет осторожно регулировать начальную скорость так, чтобы нырнуть вниз до минимального радиуса, чуть большего, чем удвоенный радиус Шварцшильда, а потом заглушит двигатель. Тогда, если только Алиса верно подберет начальную скорость, она спикирует вниз, много-много раз обернется вокруг черной дыры, а потом пробкой вылетит обратно на радиус, с которого начала падение. Для движения такого типа существует специальный термин: эллипсо-вихревая орбита
[5]. Алиса чувствует себя на таких орбитах как на крутейших американских горках: все начинается со свободного падения, а в вихревой фазе движешься довольно быстро – со скоростью около двух третьих световой. Беда в том, что эта игра для Алисы весьма опасна. Если ее начальная скорость окажется чуть-чуть меньше, так что орбита занесет ее под двойной радиус Шварцшильда, она начнет падать в черную дыру и спасти ее сможет только аварийный запуск двигателей челнока, которые вынесут челнок наружу. Но при этом двигатели должны быть запущены прежде, чем Алиса достигнет горизонта, – иначе все пропало.
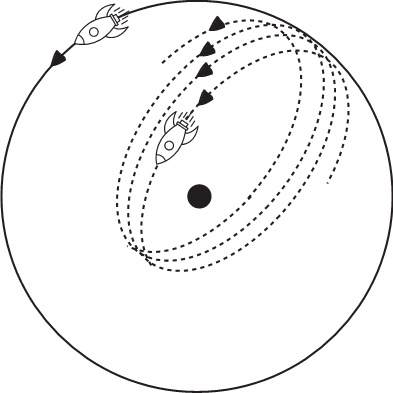
Рис. 3.2. Круговая орбита (сплошная кривая) и отрезок релятивистски прецессирующей эллиптической орбиты (пунктир). Нерелятивистская ньютоновская орбита (на рисунке не показана) выглядела бы как эллипс, находящийся на одном и том же месте; релятивистская прецессия заставляет этот эллипс постоянно перемещаться, как показано на рисунке.
После нескольких головокружительных полетов по эллипсо-вихревой орбите с большой высоты Алиса решает попробовать заманить Боба на орбиту пониже и поближе к себе, чтобы и он попробовал этот аттракцион. Но Боб – парень консервативный, он предпочитает не включать двигатели своего звездолета и оставаться только на круговых орбитах. Тут Алиса замечает странную вещь: чем ниже спускается Боб, тем дальше от черной дыры ей приходится оставаться на конце своей «пращи», не переходя в падение (что требует и включения аварийных двигателей).
В конце концов, когда Боб достигает радиуса, равного тройному радиусу Шварцшильда, Алисина игра с черной дырой – закружиться вокруг нее и выпрыгнуть обратно – совсем перестает получаться. Даже если ее начальная скорость оказывается лишь чуть-чуть меньше, чем у Боба, Алису затягивает в гравитационный колодец и ей приходится тут же вырываться из него с помощью аварийных двигателей, чтобы не быть проглоченной горизонтом. Боб теперь находится на так называемой предельной устойчивой круговой орбите вокруг черной дыры. Существуют круговые орбиты и с меньшими радиусами, но все они неустойчивы, а это означает, что малейшее возмущение может заставить находящегося на этой орбите нырнуть в черную дыру. Боб, естественно, на них переходить отказывается. А ведь это как раз те самые орбиты, по которым Алиса стремительно проносилась мимо черной дыры в свободном падении во время своих вихревых полетов.
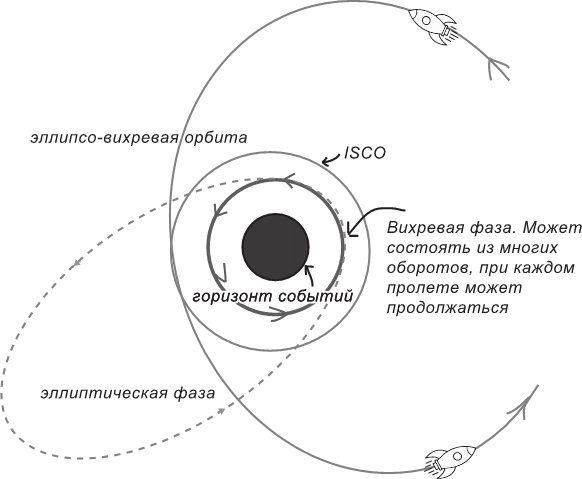
Рис. 3.3. Эллипсо-вихревая орбита.
Аббревиатурой ISCO (innermost stable circular orbit) обозначена предельная устойчивая круговая орбита.
Теперь давайте посмотрим, какие сигналы видит Боб, наблюдая за орбитальными акробатическими трюками Алисы. Не забудем, что у нее есть специальная желтая мигалка! Но сначала остановимся на минутку и поговорим об эффекте доплеровского сдвига, который наблюдается даже в отсутствие тяготения. По сути, для его объяснения не нужна и специальная теория относительности. Например, когда вы слышите сирену приближающейся машины скорой помощи, то в момент, когда она проезжает мимо вас, вы замечаете, что тон звука изменился. Для простоты представьте, что у сирены вполне определенный тон, например ля первой октавы, то есть 440 герц, 440 звуковых колебаний в секунду, и что автомобиль мчится со скоростью в одну десятую скорости звука (это довольно быстро, но возможно: примерно 120 километров в час). Когда «скорая» едет по направлению к вам, тон ее сирены примерно на 10 % выше, чем 440 герц, а когда она проехала мимо и удаляется, примерно на столько же ниже. Вот это изменение тона и есть эффект Доплера. Объясняется он тем, что когда «скорая» приближается, каждое последовательное звуковое колебание рождается чуть ближе к вам, чем предыдущее. Поэтому для вас частота колебаний становится немного больше, когда их источник приближается, чем когда он неподвижен. Похожий эффект происходит и со светом в специальной теории относительности. Если при отсутствии гравитационного поля Алиса летит прямо к Бобу, электромагнитные колебания, из которых состоит желтый свет ее мигалки, покажутся ему имеющими чуть большую частоту – или более короткую длину волны. А это значит, что желтый свет будет видеться ему скорее голубым. Соответственно, когда Алиса летит от Боба, желтые лучи ее мигалки для него будут выглядеть красноватыми. По той же причине вспышки, которые посылает ему мигалка Алисы каждую секунду (по ее часам), Боб будет принимать чаще, чем раз в секунду, когда Алиса летит к нему, и реже – когда от него. Тут может прийти мысль, что в специальной теории относительности эффект Доплера должен как-то объединяться с замедлением времени – что и происходит в действительности, и мы как раз это подробно описали.




