Принимая всё это во внимание, поговорим еще раз о странностях, связанных с наиболее гладким из всех возможных вариантов математического расширения решения Керра за внутренний горизонт. Пересекая его, зонд оказывается в новой ветви Вселенной. В этой части Вселенной сингулярность всегда видима и не существует горизонта событий. Сингулярность имеет форму вращающегося кольца, кривизна и приливные силы которого обращаются в бесконечность, когда мы к нему приближаемся. Однако, в отличие от сингулярности в решении Шварцшильда, которая появляется в некоторый момент будущего на любой возможной траектории падения, керровская кольцевая сингулярность имеет определенную пространственную локализацию, и зонд может избежать входа в нее. Для этого у него есть несколько способов. Один из них – снова начать двигаться вовне к большим значениям радиуса, всё дальше от радиуса внутреннего горизонта. В этом сценарии пространство-время втянет зонд в область белой дыры и быстро выбросит наружу, когда эта часть пространства-времени эволюционирует в новую керровскую черную дыру с массой и вращением, идентичными параметрам дыры, чей горизонт событий зонд первоначально пересек. Зонд никогда не сможет вернуться в белую дыру, потому что, как и в шварцшильдовском случае, она теперь в его прошлом, а в будущем остается только новая черная дыра. Однако зонд может бесконечно повторять одни и те же стадии движения: нырять в очередную черную дыру, пересекать ее внутренний горизонт, а затем возвращаться назад через новую белую дыру, чтобы снова попасть в черную. Аналитическое расширение решения Керра, таким образом, дает нам бесконечную последовательность Вселенных, состоящих из черных дыр, соединенных белыми.
Для зонда, который пересек внутренний горизонт, есть и другая возможность: продолжать двигаться внутрь и пройти сквозь кольцевую сингулярность. Прекрасно, нет ничего проще! Это все равно, что прыгнуть сквозь обруч. Но разве нельзя было бы оказаться в том же месте, не прыгая сквозь обруч, а просто обойдя его вокруг? Как ни странно, нельзя! Условие максимальной гладкости требует, чтобы после прыжка сквозь обруч зонд оказался бы в совершенно другой области Вселенной. Она тоже может описываться метрикой решения Керра с теми же характеристиками вращения, но на этот раз за вычетом массы исходной керровской черной дыры. Другими словами, в этом месте в пространстве-времени находится «голая» сингулярность отрицательной массы. Эффективная гравитационная сила, обусловленная этой сингулярностью, на самом деле является силой отталкивания, и тела, двигаясь по геодезическим, не падают на нее, а движутся от нее прочь. Что еще более странно, существует область пространства-времени, в которой есть так называемые замкнутые времениподобные кривые. Пример замкнутой кривой – кольцо: у него конечная длина, оно начинается в любой своей точке, и проход по нему приводит в исходное положение. Но «нормальные» замкнутые кривые пространственноподобны. Если вы движетесь по кольцу, вы тем самым одновременно движетесь и вперед во времени: поэтому когда вы возвращаетесь в стартовое положение, вы оказываетесь в той же точке пространства, но во времени вы ушли в будущее по отношению к моменту старта. Это времениподобная кривая, и она не замкнута. С замкнутой времениподобной кривой дело обстоит иначе: когда вы возвращаетесь в начальное положение, вы на деле находитесь снова в том же пространственно-временном событии, с которого вы начинали.
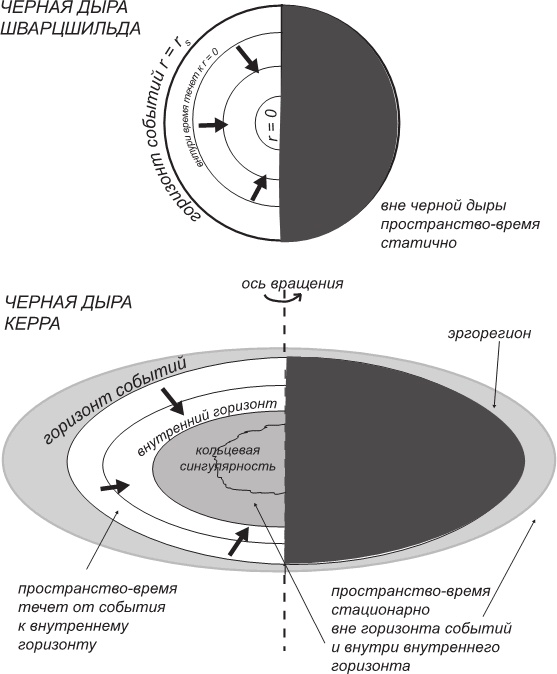
Рис. 4.3. Схематический вид внутренней структуры черных дыр.
В сущности, в области замкнутых времениподобных кривых работает машина времени. Вдалеке от сингулярности не существует никаких замкнутых времениподобных кривых, и если не считать сил отталкивания в районе сингулярности, пространство-время выглядит совершенно обычно. Однако существуют траектории движения (они не геодезические, так что вам понадобится ракетный двигатель) которые доставят вас в область замкнутых времениподобных кривых. Как только вы окажетесь там, вы сможете двигаться в любом направлении по координате t, которая показывает время удаленного наблюдателя, но по вашему собственному времени вы все равно всегда будете двигаться вперед. А это значит, что вы можете отправиться в любой момент времени t, в который захотите, а потом вернуться в удаленную часть пространства-времени – и даже прибыть туда до того, как отправитесь. Конечно, теперь оживают все парадоксы, связанные с идеей путешествий во времени: например, что, если бы, совершив прогулку во времени, вы убедили ваше прошлое «я» отказаться от нее? Но могут ли существовать такие виды пространства-времени и как могут быть разрешены связанные с этим парадоксы – вопросы, выходящие за рамки этой книги. Однако, так же как и в случае с проблемой «голубой сингулярности» на внутреннем горизонте, общая теория относительности содержит указания на то, что области пространства-времени с замкнутыми времени-подобными кривыми неустойчивы: как только вы попытаетесь совместить с одной из этих кривых какое-то количество массы или энергии, эти области могут стать сингулярными. Более того, во вращающихся черных дырах, образующихся в нашей Вселенной, именно «голубая сингулярность» сама по себе может не дать образоваться области отрицательных масс (и всем керровским другим вселенным, в которые ведут белые дыры).
Тем не менее то, что общая теория относительности допускает такие странные решения, выглядит интригующе. Их, конечно, легко объявить патологией, но не забудем, что сам Эйнштейн и многие его современники говорили то же самое о черных дырах.
Мы закончим эту главу кратким обсуждением заряженных черных дыр. Мы уже говорили о формуле «черные дыры не имеют волос»; другими словами, они не оставляют в структуре пространства-времени никаких сведений о том, что в них упало. Можно сказать, у них плохая память: они могут вспомнить только общую массу и момент импульса тел, которые они проглотили. Но что, если мы бросим в черную дыру электрон? И если черная дыра о нем тоже забудет, что произойдет с его электрическим зарядом? Разве его исчезновение не было бы нарушением закона сохранения заряда, священного правила физики частиц? Конечно, было бы. Но, к счастью, у черных дыр могут быть добавочные «волосы» для сил дальнодействия, с которыми связано сохранение заряда. Эти силы описываются теорией электромагнетизма. Решения уравнений электромагнетизма, найденных Максвеллом, в сочетании с уравнениями поля Эйнштейна, описывающими вращающиеся и заряженные черные дыры, дают так называемую метрику Ньюмена, однозначно определяемую массой, спином и электрическим зарядом. Вообще-то, решение, описывающее невращающуюся заряженную черную дыру, было получено много лет назад: такой объект в честь его первооткрывателей называется черной дырой Рейснера – Нордстрёма. Это решение удалось получить намного раньше по той причине, что, как и в решении Шварцшильда, невращающееся пространство-время черной дыры Рейснера – Нордстрёма сферически симметрично, и поэтому уравнения поля в математическом отношении значительно проще. Интересно, что заряд, даже и сам по себе, сообщает внутренней структуре черных дыр свойства, подобные тем, которые обусловлены наличием момента импульса. В черных дырах Рейснера – Нордстрёма есть и внутренний горизонт, и «голубые сингулярности», и множественные связанные Вселенные. Однако в отсутствие вращения кольцевые сингулярности сжимаются в точку, и поэтому в пространстве-времени Рейснера−Нордстрёма нет областей отрицательной массы с замкнутыми времениподобными кривыми в них.



