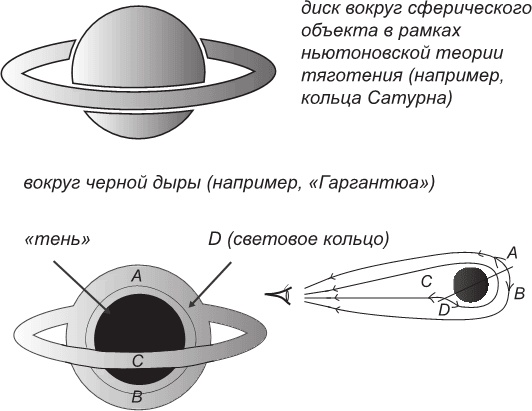
Рис. 5.2. «Тень» черной дыры. В теории тяготения Ньютона (вверху) лучи света, выходящего из диска вокруг массивного объекта, не искривляются. В этом случае мы видим неискаженное изображение доступной взгляду части диска. Вокруг черной дыры (внизу) кривизна пространства-времени настолько велика, что лучи света сильно искривляются – настолько, что мы видим все части диска, включая те, что находятся за черной дырой. Траектории нескольких из этих световых лучей показаны внизу справа, что позволяет построить изображение, приведенное внизу слева.
Мы закончим эту главу кратким упоминанием одного увлекательного астрономического проекта. Он называется «Телескоп горизонта событий», и в его рамках сделана попытка получить изображения так называемой тени сверхмассивной черной дыры в центре нашей Галактики. Кроме того, с ним планируются наблюдения черного монстра массой более чем в миллиард Солнц в галактике M87, которая расположена относительно близко к нам: на расстоянии всего немногим более 50 миллионов световых лет. Эти две черные дыры выбраны для наблюдений потому, что из всех известных черных дыр их шварцшильдовские радиусы имеют самые большие угловые размеры на небе. Для черной дыры в Sgr A* это объясняется тем, что она находится очень близко к нам (относительно, конечно), а для дыры в M87 – тем, что она такая огромная. Телескоп горизонта событий представляет собой группу больших радиотелескопов, разбросанных по всему земному шару и работающих как единый инструмент. Это позволяет реализовать что-то вроде измерения параллакса: одновременно регистрируя на разных телескопах радиоволны от одного и того же источника в рамках метода, называемого интерферометрией, можно достичь такого углового разрешения, какое было бы у телескопа размером с весь земной шар. Поэтому такие интерферометры способны разглядеть у космических объектов крайне мелкие детали, что и необходимо, если мы хотим увидеть окрестности горизонта черной дыры! Например, угловые размеры горизонта событий источника Sgr A* составляют всего 6 наноградусов. Пытаться рассмотреть такие детали – все равно что различить в телескоп цифры на поверхности серебряного доллара, лежащего на поверхности Луны! Правда, интерферометрические методы не способны обеспечить составному телескопу ту же светособирающую силу, которую имел бы гипотетический телескоп размером с Землю (мы можем использовать только тот свет, который собрали все антенны наших индивидуальных телескопов, вместе взятые). Но для целей, которые мы преследуем, наблюдая Sgr A* и M87, именно разрешающая сила наиболее важна. Конечно, наши телескопы не смогут «увидеть» ни одной из самих черных дыр. Но зато они смогут зарегистрировать свет, выходящий из вихрящихся вокруг них аккреционных дисков. Этот свет (большая его часть) будет следовать геодезическим пространства-времени черной дыры. Но, как мы видели в главах 3 и 4, очень близко к горизонту сворачивание пространства-времени столь сильно, что траектории фотонов будут крайне искривлены, а некоторые из фотонов, прежде чем отправиться к нам, даже опишут несколько оборотов вокруг черной дыры, вблизи ее светового кольца. В результате аккреционный диск будет выглядеть довольно сильно искривленным. Внутренняя круговая часть его изображения, соответствующая области, в несколько раз превышающей размер радиуса Шварцшильда, будет казаться темнее (назовем это «тенью»), за исключением яркого ободка, отмечающего положение светового кольца. Если мы смотрим на аккреционный диск с ребра, ближняя к нам часть диска будет пересекать его «тень». Кроме того, над и под тенью мы, по сути, сможем увидеть часть диска позади черной дыры – снова оттого, что в процессе выхода наружу фотоны движутся по изогнутым траекториям.
Глава 6
Столкновения черных дыр
В главах 3–5 мы говорили о черных дырах, находящихся вдали друг от друга, другими словами, об изолированных черных дырах. Нам было важно понять, как звезды обращаются по орбитам вокруг сверхмассивных черных дыр и как вокруг черных дыр образуются аккреционные диски – эти вопросы были и остаются очень интересными, так как именно такие явления наилучшим образом доказывают само существование черных дыр. Во всяком случае, это было так – до тех самых пор, пока детектор LIGO не зарегистрировал гравитационные волны от столкновения двух черных дыр, которое произошло более миллиарда лет назад на расстоянии в примерно столько же световых лет
[15]. В этой главе мы расскажем о теории, объясняющей наблюдавшееся событие. Что такое гравитационные волны? Почему сталкиваются черные дыры и почему эти столкновения порождают гравитационные волны? Почему прошло целых сто лет с тех пор, как Эйнштейн опубликовал свою общую теорию относительности, до момента, когда ученые сумели впервые прямо их зарегистрировать?
Столкновения черных дыр – самые мощные явления, какие только возможны в рамках общей теории относительности. Ни в каких других событиях во Вселенной не выделяется столько энергии. Большой взрыв, с которого началась история Вселенной, конечно, был еще мощнее, но для того, чтобы описать начало времени как такового, требуется еще более всеобъемлющая теория, чем общая теория относительности. И физики еще только нащупывают правильный теоретический подход, в рамках которого можно было бы дать полное описание Большого взрыва. Столкновения черных дыр не требуют создания более общих теорий, чем уже существующие: судя по всему, вполне достаточно просто уравнений Эйнштейна, Gµν = 8πGNTµν/c4. Более того, во многих случаях столкновений черных дыр мы, вероятно, можем не принимать во внимание тензор энергии-импульса Tµν, который обращается в нуль при отсутствии какого-либо вещества: полная энергия вещества вокруг черных дыр исчезающе мала по сравнению с энергией покоя самих черных дыр. Следовательно, чтобы описать столкновения черных дыр, нам надо всего лишь решить систему уравнений исключительно простого вида: Gµν = 0. На знаменитой фотографии Эйнштейна он как раз записывает эквивалентную систему Rµν = 0, где Rµν – так называемый тензор Риччи, тесно связанный с тензором Эйнштейна и по сути эквивалентный ему при отсутствии вещества. Правда, на фото (рис. 6.1) Эйнштейн пользуется индексами i и k, но это дело вкуса: он вполне мог бы написать и Rµν = 0.
Хоть мы уже и обсуждали эйнштейновские уравнения поля, но прежде чем приступить к подробному разбору столкновений черных дыр, стоит пересмотреть наши интуитивные представления о том, что эти уравнения описывают. Коротко можно сказать, что уравнения поля выражают в математической форме способ, которым вещество определяет искривление пространства-времени. Что уравнения поля позволяют пространству-времени делать, когда вещество отсутствует? Один из примеров разрешенных в этом случае состояний пространства-времени – это просто отсутствие какой-либо кривизны. Другими словами, совершенно плоское пространство-время является решением уравнений Эйнштейна в вакууме, но это решение не единственное. Действительно, есть и другой пример конфигурации пространства-времени, допускаемой уравнениями поля в вакууме: изолированная черная дыра. Как мы видели, внутри горизонта черной дыры могут существовать сингулярности или другие необычные особенности, которые можно было бы связать с ненулевым тензором энергии-импульса. Но снаружи горизонта вполне возможно полное отсутствие всякого вещества. У нас нет никаких обязательств по поводу внутренности черной дыры, так как оттуда до нас все равно не могут дойти никакие сигналы. Поэтому из соображений экономии проще всего считать, что изолированная черная дыра – это пример искривления пространства-времени даже и при отсутствии вещества. Пара черных дыр, обращающихся друг вокруг друга, дает нам еще один пример решения уравнений поля в вакууме. Такие черные дыры будут постепенно сближаться друг с другом по спирали и в конце концов сольются в быстро вращающуюся керровскую черную дыру. Именно такое событие и наблюдалось на установке LIGO 14 сентября 2015 года.



