Бекенштейн сформулировал необыкновенно сильное утверждение: черные дыры несут в себе больше энтропии, чем любая другая форма вещества, способная занять тот же объем пространства-времени. Более простая версия этого утверждения выглядит так: для того, чтобы обычное вещество, уложенное в конечную область пространства-времени, обладало большой энтропией, этого вещества должно быть очень много – настолько, что дело начинает пахнуть гравитационным коллапсом. Прежде чем энтропия обычного вещества превысит теоретическую энтропию черной дыры, это вещество сколлапсирует в черную дыру. В этом смысле коллапс в черную дыру представляет собой самое неупорядоченное и необратимое событие из всех возможных.
Микроскопическое обоснование закона площадей предлагает – при некоторых ограниченных условиях – теория струн, но в целом этот закон из фундаментальных физических принципов не выводится. Однако Тед Якобсон утверждает, что если мы будем исходить из термодинамики черных дыр, в частности из закона площадей, объединив этот подход с некоторыми основными положениями дифференциальной геометрии, то придем к уравнениям Эйнштейна – основе общей теории относительности. Более того, известно, что если модифицировать уравнения Эйнштейна с сохранением их внутренней симметрии, закон площадей изменится, а вычисления Хокинга по сути останутся теми же. Так что выходит, что энтропия черной дыры – хороший инструмент для описания динамики пространства-времени. И все-таки, что же представляет собой энтропия черной дыры?
Недавно Хуан Малдасена и Леонард Сасскинд внесли предложение, которое должно более тесно увязать энтропию запутанности с энтропией черной дыры. Вот в чем это предложение состоит. Вспомним парадокс ЭПР, где два спина были вначале запутаны, а затем разделены, и парадоксальным образом ни один из них не имел определенного квантового состояния сам по себе, хотя оба вместе его имели. Каждый спин является кубитом, и каждый сам по себе имеет равное кубиту количество энтропии. Не могли бы мы предположить, что на некотором микроскопическом уровне каждый из них является черной дырой и что их запутанность геометрически проявляется в виде кротовой норы между ними? Тут есть два очевидных возражения. Во-первых, черная дыра только с одним кубитом энтропии так мала, что геометрические соображения могут для нее не иметь никакого значения. Во-вторых, как уже говорилось в главе 3, кротовые норы непроходимы. Чтобы понять, как можно обойти эти возражения, давайте сначала представим себе системы большего размера с большим числом возможных квантовых состояний и, следовательно, с большими значениями энтропии. Но при этом будем настаивать на том, что две из этих более крупных систем, которыми распоряжаются, как обычно, наши Алиса и Боб, идеально запутаны, так что их объединенное квантовое состояние точно определено. Выше мы в качестве примеров систем больших размеров брали бруски чистого магния, но теперь мы хотим использовать более сложное состояние вещества, которое через некоторое время должно сколлапсировать в черную дыру. Короче говоря, Алиса и Боб оказываются вдалеке друг от друга, каждый по отдельности в окрестности своей черной дыры, и по крайней мере значительная часть энтропии каждой из этих черных дыр обязана своим существованием квантово-механической запутанности между этими двумя системами. Затем мы предполагаем, что эти черные дыры соединены кротовой норой, и она является геометрическим проявлением их запутанности.
Но как можно было бы проверить эту идею? Рассмотрим мысленный эксперимент, в котором и Алиса, и Боб занимаются измерениями каждый в своей системе. Изучать на близком расстоянии систему, в которой происходит гравитационный коллапс, – рискованная затея, так как, по всей вероятности, в процессе измерений наблюдатель будет всосан в черную дыру. Это безрадостная перспектива даже в концептуальном смысле, так как она исключает возможность для Алисы и Боба выполнить свои измерения и затем сравнить их результаты для того, чтобы убедиться, что их системы действительно были запутаны.
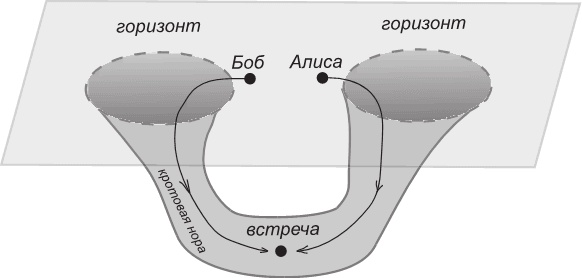
Рис. 7.3. Кротовая нора, соединяющая области пространства-времени вблизи Алисы и Боба соответственно. Кротовые норы, возникающие из запутанных квантовых состояний, позволяют Алисе и Бобу встретиться друг с другом, прыгая в черные дыры. Затем они еще могут успеть сверить свои квантовые запутанности, прежде чем их ждет роковое поглощение сингулярностью черной дыры.
Но постойте! Мы же допустили, что две наши черные дыры соединены кротовой норой! Алиса и Боб действительно могут быть затянуты в недра своих черных дыр, но так как их соединяет кротовая нора, то на самом деле эти черные дыры имеют одно и то же внутреннее пространство. Для единственного наблюдателя невозможно перебраться по кротовой норе из одного внешнего пространства в другое, но это оказывается вполне возможно для двух наблюдателей, которые входят в кротовую нору с двух противоположных концов внутреннего пространства и встречаются. Так что выходит, Алиса и Боб все же могли бы сравнить свои измерения. Это важный аргумент в первую очередь в пользу возможности образования кротовой норы: ведь если бы такая нора не могла образоваться, Алиса и Боб не могли бы сравнить результаты своих измерений, и сам принцип квантовой запутанности оказался бы в опасности. Для Алисы и Боба такой аргумент был бы слабым утешением, потому что за конечное время падения в свои черные дыры они бы столкнулись с обычными для черных дыр сингулярностями. Но, по крайней мере, они могли бы под конец выполнить последнюю и окончательную проверку принципов квантовой механики!
Отступим на минуту от этих интенсивных теоретических обсуждений и зададим резонный вопрос: есть ли хоть какой-то практический интерес в мысленных экспериментах только что описанного вида, в ходе которых наблюдателям приходится прыгать в черные дыры? Наблюдатели, остающиеся снаружи, никогда не смогут удостовериться (по крайней мере, классическими средствами) в том, встретились Алиса и Боб или нет. Может, все это просто схоластика? По общему мнению теоретиков, нет. Мы должны помнить о том, что горизонты черной дыры – это вопрос нашей будущей судьбы, а не сиюминутного опыта. Возможно, мы все в этот момент пересекаем горизонт космической черной дыры, чья сингулярность отстоит от нас в будущем на большее время, чем то, которое отделяет нас от начала Вселенной. Многие космологи провидят в конце непрекращающегося расширения Вселенной ее окончательный коллапс. Так не может ли некоторое созидательное разрушение в конце самого пространства-времени открыть нашему восприятию нечто, о чем мы сейчас не можем и мечтать?
Эпилог
Мы не верим в путешествия во времени и не склонны к мистицизму. Но что, если бы мы могли написать письмо Альберту Эйнштейну, чтобы рассказать ему в нескольких словах о тяготении и черных дырах? Мы написали бы что-то вроде следующего.
Июль 2017
Дорогой Альберт, Прежде всего, Вы величайший гений. Ваше E = mc²– единственное физическое уравнение, известное буквально всем. Журнал «Тайм» назвал Вас человеком столетия. Анекдотов про Эйнштейна больше не рассказывают просто потому, что с первого слова все уже знают, в чем соль. Благодаря Вашим открытиям человечество наделало сикстильон сикстильонов ядерных зарядов и, как ни странно, пока еще с их помощью само себя не взорвало. Фактически атомные бомбы, сброшенные в конце Второй мировой войны, так и остались единственными ядерными зарядами, использованными для уничтожения людей.

