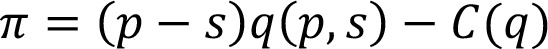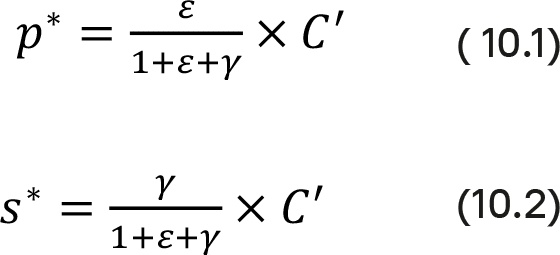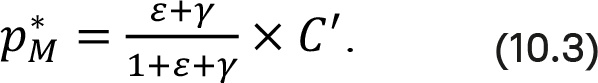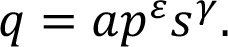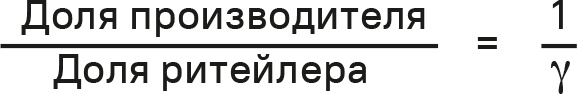Чтобы получить комбинацию конечной потребительской цены и маржи ритейлера, максимизирующую прибыль, нужно дифференцировать функцию прибыли производителя:
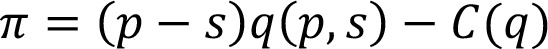
относительно p и s. После нескольких шагов получаем
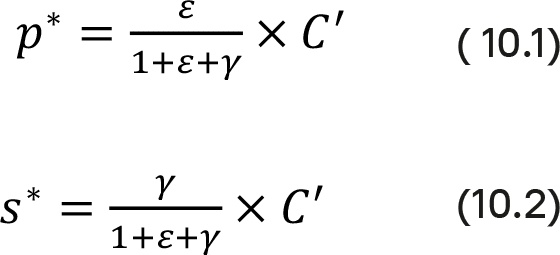
где C' – это, как обычно, маржинальные затраты, а ε и γ – эластичности цены и маржи. Поскольку продажная цена производителя – это разница между конечной ценой p и маржой s, получаем
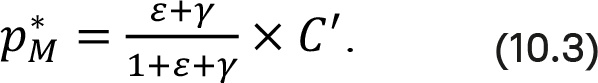
Оптимальные условия одновременной оптимизации потребительской цены и маржи можно, таким образом, сформулировать аналогично формуле Аморозо – Робинсона (5.2).
Из этих условий выводим следующие утверждения при прочих равных.
• Чем меньше ценовая эластичность ε в абсолютном выражении, тем выше конечная потребительская цена p*, маржа s* и продажная цена производителя p*M.
• Чем выше эластичность маржи γ, тем выше конечная потребительская цена p*, маржа s* и продажная цена производителя p*M. Относительно конечной цены p* эластичность маржи имеет тот же эффект, что и снижение ценовой эластичности.
• Продажа через ритейлеров или посредников дает повышенную конечную цену по сравнению с ценой через прямые продажи, когда производитель устанавливает и конечную потребительскую цену p, и маржу дилера s, при этом эластичность маржи положительная. Однако, согласно данному утверждению, здесь нет переменных сбытовых издержек. Они могут быть выше в прямых продажах, чем в непрямых.
• По мере снижения ценовой эластичности ε маржа s* растет сильнее, чем продажная цена производителя p*M и удельная маржинальная прибыль, если эластичность маржи выше 1. Для γ < 1 справедливо противоположное.
• По мере роста эластичности маржи γ маржа s* растет быстрее, чем продажная цена производителя p*M, если ценовая эластичность больше 2 (абсолютное значение).
Если у ритейлера переменные сбытовые издержки k на единицу продукции, то в производном выше можно заменить валовую маржу (p – pM) чистой маржой (p – pM – k). Далее выполняются аналогичные производные, и утверждения о влиянии эластичности цены и маржи не меняются.
В табл. 10.1 обобщаются качественные рекомендации для политики конечных цен маржей, если мы будем рассматривать категории «высокая» и «низкая» для эластичности цены и маржи.
Чтобы это проиллюстрировать, возьмем постоянные значения эластичности, выведенные по следующей формуле «цена-отклик»:
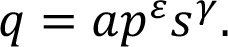
С учетом постоянных маржинальных затрат С правила решения (10.1) и (10.2) можно применять напрямую. На рис. 10.2 показаны оптимальная цена для конечных пользователей и продажная цена производителя как функция ценовой эластичности ε и эластичности маржи γ, разница между двумя кривыми соответствует марже s*. С помощью этого рисунка можно легко верифицировать вышеприведенные утверждения.
Таблица 10.1. Качественные рекомендации по политике конечных цен и маржей производителя
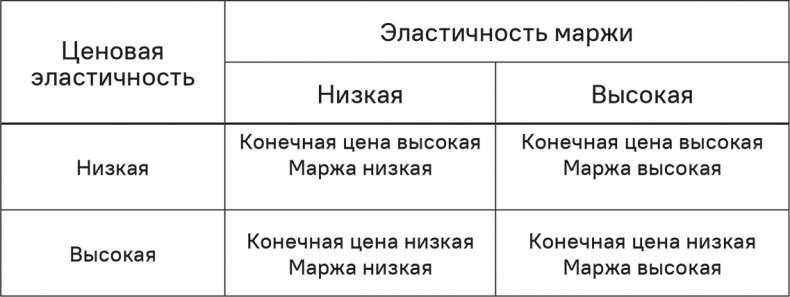
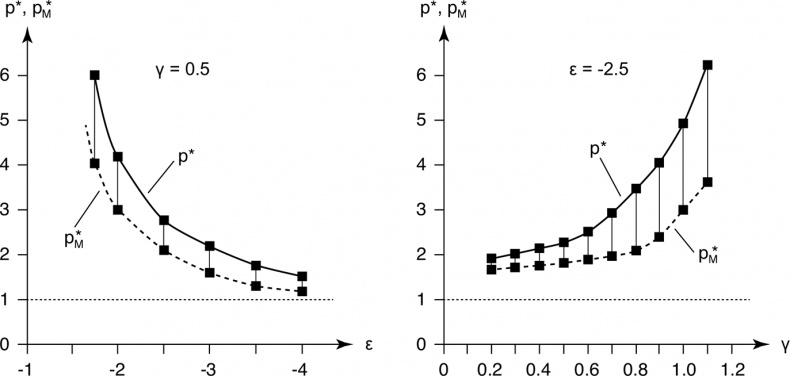
Рис. 10.2. Эффекты изменений эластичности для оптимальных цен и маржей
10.2.1.2. Доля производителя и ритейлера
Вопрос о том, как делится оптимальная общая маржа (p* – C') между производителем и ритейлером, весьма интересен. Доля производителя в общей марже = (p*M – C') / (p* – C'). Если вставить p*M и p* из (10.3) и (10.1) и упростить, получим выражения:
1 / (1 + γ) как долю производителя
и γ / (1 + γ) как долю ритейлера.
Соотношение долей производителя и ритейлера:
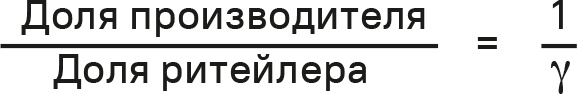
Данное соотношение не зависит от ценовой эластичности. Маржа производителя и маржа ритейлера идентичны, если эластичность маржи равна 1. При γ > 1 ритейлер имеет большую долю в общей марже (p* – C'), а при γ < 1 – производитель. Данный результат имеет смысл, поскольку при γ > 1 предельное снижение маржи производителя избыточно компенсируется объемом дополнительных продаж за счет повышения эластичности маржи.
10.2.1.3. Маржа как инструмент конкуренции
Маржа ритейлера может стать важным инструментом конкуренции в типовой ситуации, когда много продуктов конкурируют на уровне розницы за место на полках и спрос конечных потребителей.
Это особенно важно в ситуациях, когда потребитель уже принял в основном решение о покупке, но до сих пор не определился с брендом, и ритейлер может влиять на его выбор.
Если цена и качество конкурирующих продуктов примерно одинаковы (и в последнем случае покупатель часто не уверен в своем суждении), ритейлер порекомендует продукт, обеспечивающий высокую маржу. Все виды вышеприведенного анализа можно применить к конкуренции. Теория олигополии в отношении цены также применима к марже. Это значит, что можно определять перекрестные эластичности так же, как и функции отклика. Так как это предусматривает инверсию выводов по цене, перенести выводы по цене на маржу относительно несложно. Поэтому не будем здесь приводить подробных разъяснений.
На практике магазинные бренды, дженерики и товары без брендового имени в процентном (и иногда в абсолютном) выражении имеют более высокую маржу, чем классические брендовые товары. С точки зрения конкуренции стратегия маржи отличается от (открытой) ценовой стратегии с точки зрения прозрачности. Поскольку маржой можно управлять с помощью индивидуальных и, следовательно, не раскрываемых уступок (зачастую в виде неких бонусов), использование этого инструмента менее прозрачно для конкурентов, чем открытые, то есть публичные, изменения цен. Поэтому маржа – это выгодная отправная точка для завуалированных или обособленных мер увеличения рыночной доли.
10.2.1.4. Эмпирические аспекты эластичности маржи
Изложенные нами до сих пор теоретические соображения дают полезную информацию относительно связей между эластичностью маржи и оптимальными ценами и торговыми наценками. Но с практической точки зрения здесь требуются численные значения эффектов маржи. Если известна конкретная функция «цена-отклик», измерить соответствующие параметры влияния маржи в принципе несложно. Так же, как и для ценовых эффектов, для измерения можно воспользоваться эконометрическими методами или экспертными суждениями. Опросы потребителей здесь не принесут пользы.