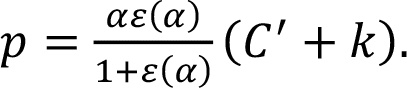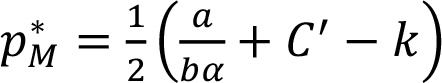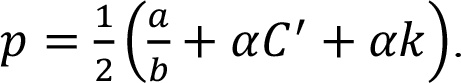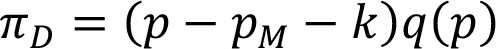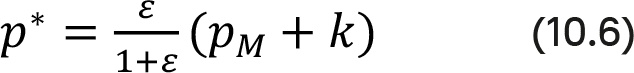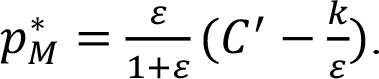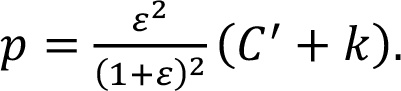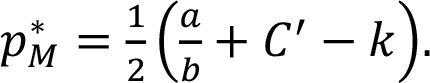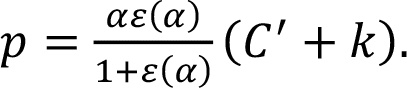
Для изоэластичной функции «цена-отклик» конечная потребительская цена выше, чем при прямых продажах, при условии таких же маржинальных затрат на дистрибуцию и если α > 1.
Для линейных функций «цена-отклик» можно сформулировать особые утверждения. Оптимальные значения будут следующие:
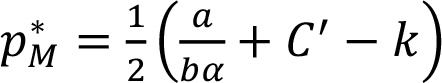
и
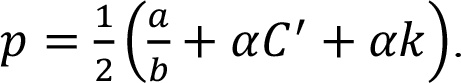
pM меньше, p больше оптимальной цены при прямых продажах при условии одинаковых сбытовых издержек. Чем выше коэффициент надбавки, тем ниже продажная цена производителя и тем выше конечная потребительская цена.
На рис. 10.3 показана ситуация с прибылью и разбивка прибыли между производителем и торговым партнером для линейной функции «цена-отклик». Результаты основаны на функции «конечная цена-отклик» q = 100 – 10p, постоянных маржинальных затратах C' = 4 и переменных сбытовых издержках k = 0. Мы исходим из торговой наценки в 25 % (α = 1,25).
Оптимальная конечная потребительская цена p* = $7,50, оптимальная продажная цена производителя p*M = $6. Прибыль производителя – $50, прибыль торгового партнера – $37,50. Ни одной из сторон не удается выйти на максимально возможную прибыль.
Графики прибыли обеих сторон показывают, что существуют серьезные конфликты интересов. Справа от p = $7,50 обе стороны заинтересованы снижать цены, слева интересы обеих сторон противоречат друг другу. Торговому партнеру нужна возможно более низкая конечная потребительская цена, но это, благодаря используемому им методу «издержки плюс», возможно только при наиболее низкой продажной цене производителя. В таких ситуациях торговый партнер оказывает сильное давление на производителя.
Противодействующие влияния на прибыль производителей и торговых партнеров в низкоценовой области объясняются тем фактом, что значения удельной маржинальной прибыли (относительно объемов) меняются для производителей совсем по-другому, чем для торговых партнеров. При конечной потребительской цене p = $7 (продажная цена для потребителя pM = $5,60) торговый партнер и производитель получают удельную маржинальную прибыль $1,60 и $1,40 соответственно.
Если p снижается до $6, а pM до $4,80, удельная маржинальная прибыль торгового партнера падает на $0,40 до $1,20 (–25 %), а этот показатель для производителя падает на $0,60 до $0,80 (–42,8 %). Объем продаж за счет снижения цены на $1 растет на 30–40 единиц, то есть на +33,3 %. В процентном выражении увеличение объема выше, чем падение удельной маржинальной прибыли торгового партнера, которому при этом выгоднее сниженная цена. Но для производителя справедливо обратное, поскольку его удельная маржинальная прибыль падает быстрее, чем растет объем продаж. Это снижает прибыль производителя. Данный вывод совпадает с эмпирическими наблюдениями, подтверждающими, что торговые партнеры сильно заинтересованы в высоких объемах продаж.
10.2.2.3. Оптимизация продажной цены производителя, если торговый партнер ориентирован на максимизацию прибыли
Торговый партнер определяет конечную цену для потребителей при условии, что удельные сбытовые издержки = k, так, что его прибыль
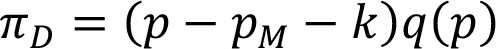
достигает максимума. Это значит, что применимая в данном случае формула Аморозо – Робинсона
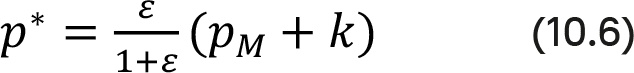
выполняется.
Производитель оптимизирует свою продажную цену за счет дифференцирования функции прибыли относительно pM, поскольку формула (10.6) вставлена для p:
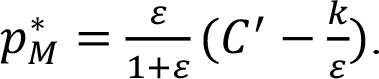
Это условие соответствует по формуле условию (10.5) для оптимальной продажной цены производителя, если торговый партнер применяет метод «издержки плюс». Для k = 0 и ε – константа производитель устанавливает продажную цену без учета торгового партнера, если цель последнего – максимизировать прибыль. Если сбытовые издержки положительные и ε – константа, продажная цена производителя выше.
Применив выражение (10.6), получаем следующую конечную цену для потребителя:
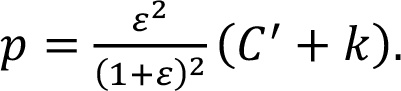
Эта цена выше оптимальной при прямых продажах, если сбытовые издержки равны. Наличие промежуточного звена в виде торгового партнера с ориентацией на максимизацию прибыли повышает конечную потребительскую цену. Мы используем линейную функцию «цена-отклик» для получения легко интерпретируемых результатов.
Оптимальная продажная цена производителя такова:
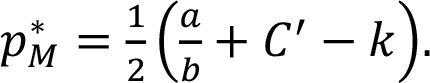
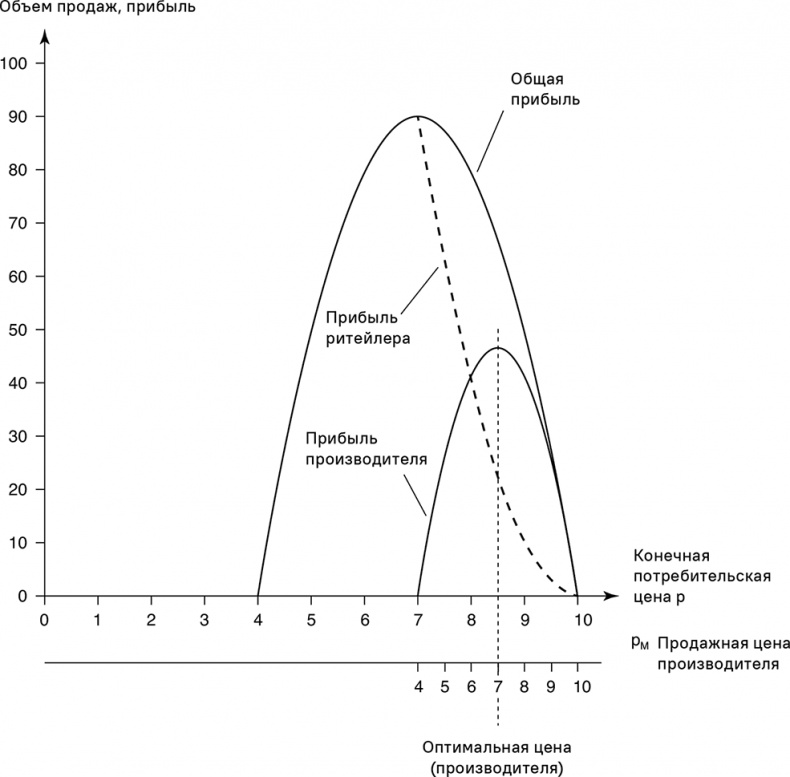
Рис. 10.4. Ситуация с прибылью и разбивка прибыли, если ритейлер максимизирует прибыль
Для k = 0, p*M идентична оптимальной цене прямых продаж, так что при этих условиях производитель может назначать свою цену с учетом торгового партнера. Если сбытовые издержки положительные, итоговая оптимальная конечная потребительская цена выше оптимальной цены при прямых продажах при одинаковых сбытовых издержках.
На рис. 10.4 показана ситуация для линейной функции q = 100 – 10p, постоянных маржинальных затрат C' = 4 и переменных сбытовых издержек k = 0.
С точки зрения производителя оптимальная конечная потребительская цена – p* = $8,50 (при оптимальной продажной цене производителя p*M = $7). Производитель получает прибыль $45, а его торговый партнер должен обходиться показателем $22,50.
Существует конфликт интересов между производителем и торговым партнером, если взглянуть налево от оптимальной конечной потребительской цены p*. Причины здесь те же, что и при методе «издержки плюс», но при сравнении двух численных примеров конфликт больше выражен в примере для торгового партнера, максимизирующего прибыль. Производитель должен снизить продажную цену на $2, чтобы оказать влияние на снижение конечной потребительской цены на $1. Производитель «жертвует» вдвое большим размером удельной маржинальной прибыли от снижения цены, чем торговый партнер.
10.2.2.4. Сравнение двух ситуаций
Используя линейные функции «цена-отклик», можно сравнивать следствия двух вариантов поведения торгового партнера. На рис. 10.5 показаны две ситуации. Сплошная линия обозначает соответствующую функцию «цена-отклик» с учетом конечной потребительской цены, а пунктирная – с учетом продажной цены производителя.