Для простоты не будем учитывать дисконтирование и постоянные затраты. Это не повлияет на нашу основополагающую аргументацию.
В первый период функция «цена-отклик» имеет вид q1 = 50 – 10p1, а во второй: q2 = 100 + λ × q1 – 10p2, где q – объем продаж, p – цена, λ – коэффициент переноса, а π – прибыль. Для различных значений λ представим соответствующие результаты в табл. 14.2, округлив до ближайших 0,5.
Таблица 14.2. Отрицательная цена с переносом
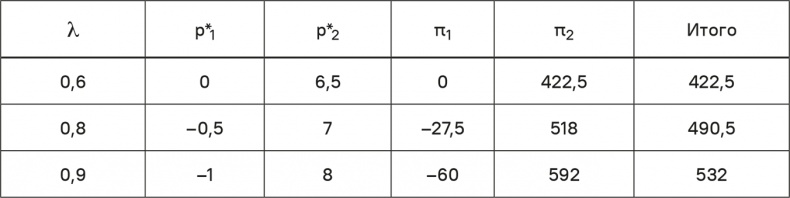
При нулевых маржинальных затратах и эффекте переноса отрицательные цены могут оказаться оптимальными. Но коэффициенты переноса могут быть относительно высокими (см. табл. 7.1 и 7.2 для сравнения), так что оптимальная цена сдвигается в отрицательную область. В эпоху цифровизации такое будет происходить всё чаще, когда маржинальные затраты равны нулю. Коэффициенты переноса для многих цифровых продуктов могут быть действительно высокими, потому что как только потребитель принимает данную систему и она его удовлетворяет, он превращается в лояльного клиента.
Можно подвести ту же аргументацию под перекрестные эффекты продуктов. Если продукт А стимулирует продажи высокоприбыльного продукта В, имеет смысл предлагать продукт А по отрицательной цене. Этот цепной эффект подходит для фримиум-структуры. Типовая фримиум-модель имеет базовую версию с нулевой ценой. Почему ценовой минимум должен иметь этот «условный» нулевой уровень? Если впечатление клиента от базовой версии действительно побудит его перейти на модель «премиум», почему бы не платить первичным пользователям или довольным клиентам за использование продукта в течение ограниченного срока, то есть предлагать им отрицательную цену вместо нулевой?
Еще один аргумент в пользу отрицательных цен – это якорная функция цен, о которой мы говорили в главе 4. Как упоминалось ранее, часто оказывалось трудно уйти от нулевой цены, особенно если потребители привыкли к ней за долгое время (например, цена ведения банковского счета или предоставления информации в Интернете). В случае отрицательной цены действие данного эффекта не такое сильное. В отличие от нулевой цены, клиенты обычно не ждут, что отрицательная цена будет держаться вечно. Они считают, что только вопрос времени, когда продавец сделает цену положительной. Если такое предположение верно, это значит, что повышение цены с –1 до 4 не приведет к столь сильному спаду объема продаж или потере клиентов, как при повышении с 0 до 4. Насколько нам известно, данная гипотеза пока не проверена.
Также можно рассмотреть роль, которую могут играть отрицательные цены в сочетании с промоушном. Это в особенности верно при внедрении новых продуктов, на которые зачастую отводятся большие рекламные средства. Правда, это не обязательно оптимальный вариант. В зависимости от относительной величины эластичностей цены и промоушна, отрицательная цена может оказаться эффективнее рекламы или аналогичных мер. Если это верно, то лучше инвестировать доступные средства в отрицательные цены, чем в иные маркетинговые инструменты. Отрицательные цены – всё еще довольно редкое явление.
Станет ли оно частым в ситуации избытка предложения, покажет будущее. Этому могут поспособствовать нулевые маржинальные затраты. Однако следует соблюдать осторожность. Отдельные клиенты пользуются к своей выгоде отрицательными ценами, не принося потом компании ожидаемой устойчивой прибыли.
14.3.8. Нулевые маржинальные затраты и шеринговая экономика
Как мы узнали из главы 5, маржинальные затраты – одна из двух детерминант оптимальной цены. Согласно формуле Аморозо – Робинсона (5.2), цена максимизации прибыли получается из зависящей от ценовой эластичности надбавки к маржинальным затратам. Для Интернета особенно характерно, что во многих случаях маржинальные затраты стремятся к нулю. Однако последнее вовсе не является совершенно новым явлением. В таких секторах, как программное оебспечение и в ряде случаев фармацевтика и электроника, маржинальные затраты по сравнению с затратами на разработку могут быть очень низкими. То же применимо к использованию мест в самолете или гостиничных номеров, когда имеются незадействованные мощности. Дополнительный гость обходится в совсем небольшие маржинальные затраты. А вот в сети явление нулевых маржинальных затрат приобретает гораздо большие масштабы. Джереми Рифкин [31] считает это явление настолько революционным, что в своей книге «Общество нулевых предельных издержек» даже утверждает, что оно может привести к «схлопыванию» или «упадку» капитализма. По примеру бывшего министра финансов США Лоренса Саммерса, он основывает свое утверждение на гипотезе о том, что цены сами по себе приближаются к уровню маржинальных затрат. Если маржинальные затраты стремятся к нулю, цены также стремятся к нулю. При этом ни один предприниматель-капиталист не захочет продавать товары или услуги по таким ценам. Эту роль должен будет взять на себя кто-то еще – например, государство или некоммерческие организации. Что и будет означать конец капитализма.
Рифкин расширяет свою парадигму нулевых маржинальных затрат на многие сектора экономики [31]. Один из них – это образовательные услуги в рамках так называемых массовых открытых дистанционных курсов. Другие сектора – это энергетика (ветровая и солнечная энергия) и шеринговая экономика. При шеринговой экономике доступные мощности, например, неиспользуемые частные комнаты или автомобили, выводятся на рынок и вводятся в экономический оборот, вместо того чтобы стоять без дела. Нет сомнения, что данное явление (не совсем новое, однако начавшее шириться подобно лесному пожару в эпоху Интернета) окажет значительное влияние на бизнес-модели и ценовые схемы. Некоторые сопутствующие эффекты уже стали реальностью, другие – еще дело будущего.
На самом деле маржинальные затраты редко бывают строго равны нулю. В своей книге Рифкин корректно использует фразу «стремящиеся к нулю маржинальные затраты» вместо более провокационной фразы, взятой в качестве заглавия [31]. Как нам известно, когда маржинальные затраты равны нулю, цена максимизации прибыли идентична цене максимизации дохода. На максимуме дохода ценовая эластичность равна –1. Согласно формуле Аморозо – Робинсона, это значение достоверно при приближении к максимуму дохода (с точки зрения маржинальных затрат). Будем исходить из функции «цена-отклик» q = 100 – 10p, где q – объем продаж, а p – цена. Для удельных затрат k = 2 цена максимизации прибыли, согласно выражению (5.3), равна p* = 6.
Доход равен $240, а если постоянные издержки нулевые, то прибыль равна $160. Ценовая эластичность равна –1,5, а коэффициент надбавки по формуле Аморозо – Робинсона равен 3.
Что случится, если маржинальные затраты упадут до 0,1? Оптимальная цена p* упадет до $5,05 и будет очень незначительно отличаться от цены макмимизации прибыли $5,00. Объем продаж вырастет до 49,5 единиц, доход до $249,98, а прибыль до $245. Ценовая эластичность при данной цене равна –1,0202, так что, согласно формуле Аморозо – Робинсона (5.2), коэффициент надбавки равен –1,0202 / –0,0202 = 50,5. Расчет 50,5 x 0,1 = $5,05 подтверждает оптимальную цену. Маржинальные затраты, стремящиеся к нулю, таким образом, не создают фундаментальных проблем в плане принятия ценовых решений. Усиление конкуренции может вместо этого стать результатом того, что нижний ценовой порог в краткосрочной перспективе находится на уровне маржинальных затрат. Следовательно, при маржинальных затратах, близких к нулю, это означает, что данный ценовой порог также стремится к нулю.

