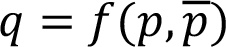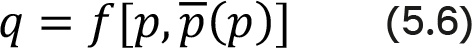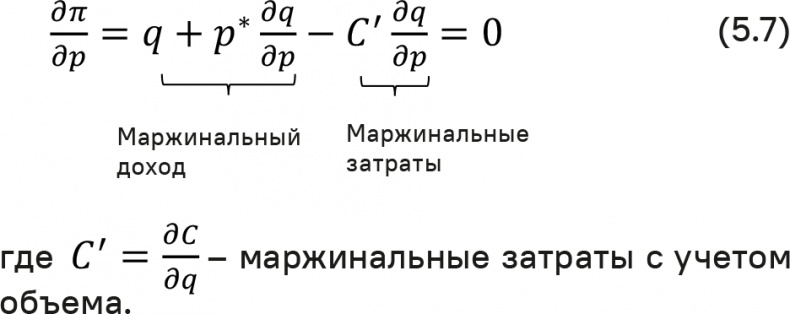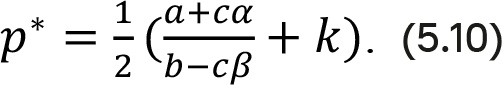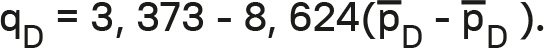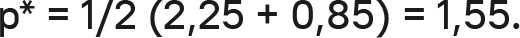Включаем функцию реакции (5.5) в функцию «цена-отклик» (без индекса продукта):
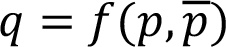
Получаем:
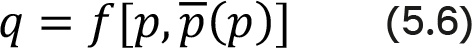
Объем продаж q здесь зависит от собственной цены p и конкурентной цены p, которая в свою очередь зависит от собственной цены. Чтобы определить оптимальную цену, мы дифференцируем функцию прибыли относительно p и устанавливаем производную, равную нулю:
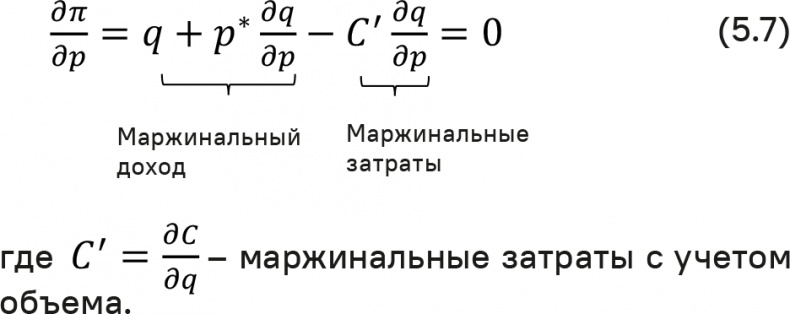
Фундаментальный принцип «маржинальный доход = маржинальные затраты» остается при олигиполии неизменным. Предприняв дополнительные шаги, мы получаем следующую формулу оптимальной цены²:

Эластичность реакции обозначает процентное изменение цены конкурентов, когда собственная цена меняется на 1 %.
В структурном смысле условие оптимальности напоминает формулу Аморозо – Робинсона (5.2). Однако на олигопольном рынке надбавка к маржинальным затратам определяется не только прямой ценовой эластичностью, но скорее «скорректированной» эластичностью, которая предусматривает конкурентную реакцию (e + sek). Выражение (e + sek) можно интерпретировать как «ценовую эластичность после конкурентной реакции».
Чтобы определить надбавку, нужно знать не только прямую ценовую эластичность, но и перекрестную эластичность и эластичность реакции.
Здесь мы снова отмечаем, что уравнение (5.8) не является решением для p*, поскольку все выражения в правой части уравнения могут зависеть от p*.
Перекрестная ценовая эластичность конкурирующих продуктов положительная. Эластичность реакции обычно бывает нулевой или положительной, то есть конкуренты либо вообще никак не отреагируют, либо сдвинут цены в том же направлении, что и инициатор изменения. В последнем случае оптимальная цена, с учетом реакции конкурентов, равна цене (или превышает ее), в которой реакция в расчет не принимается, а решения основаны на «монополистической» формуле Аморозо – Робинсона (5.2). Если эластичность реакции равна нулю, формула (5.8) удовлетворяет отношению Аморозо – Робинсона.
В случае мультипликативных функций «цена-отклик» и реакции формулу (5.8) можно использовать непосредственно как правило принятия ценовых решений. Давайте возьмем три значения: ценовая эластичность = –2, перекрестная эластичность = 0,5 и эластичность реакции = 1. Тогда уравнение дает коэффициент надбавки 3, если маржинальные затраты постоянные (то есть линейная функция затрат). Значит, надбавка к маржинальным затратам должна быть 200 %. Если перекрестная ценовая эластичность равна 0,6, процент надбавки возрастает на 250 %. Если эластичность реакции равна 0,5, при условии неизменности всех предыдущих параметров процентная надбавка будет всего 133 %. Пониженная эластичность реакции сокращает оптимальную надбавку.
Обзор
Обобщим ключевые аспекты ценовой оптимизации с учетом конкурентной реакции.
• Условия оптимальной цены при олигополии можно выразить формулой Аморозо – Робинсона.
• Оптимальная цена равна маржинальным затратам, помноженным на коэффициент надбавки, который зависит от прямой ценовой эластичности, перекрестной ценовой эластичности и эластичности реакции.
5.4.4.1. Линейная функция «цена-отклик», линейная функция реакции
Теперь рассмотрим случай линейных функций «цена-отклик» и реакции. В целом будем исходить из того, что функция затрат также линейная.
Если мы включим линейную функцию реакции

Чтобы получить оптимальную цену, можно применить правило монополистического принятия решений в формуле (5.3) к данной функции, скорректированной на реакцию:
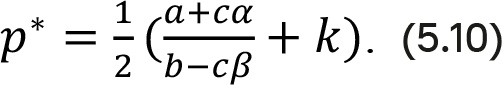
Отношение в круглых скобках соответствует максимальной цене, скорректированной на реакцию. Оптимальная цена лежит точно в срединной точке между этой максимальной ценой и переменными удельными затратами k. Оптимальная цена зависит от всех параметров в функциях «цена-отклик» и реакции.
Как и в случае с постоянными эластичностями, оптимальная цена в выражении (5.10) растет вместе с параметром конкурентной реакции b. Чем сильнее конкуренты реагируют на собственные ценовые изменения, тем выше будет оптимальная цена.
5.4.4.2. Реальный пример
Мы больше узнаем о поведении реакции, изучив реальный пример рынка бытовых чистящих средств. На рис. 5.8 показаны реальные ценовые тенденции для четырех ключевых брендов.
Рассматриваемый период времени – 2 года и 4 месяца. Как показывает визуальное наблюдение, цены на бренды A, B, C и D следовали одинаковому тренду. Отсюда следует, что имеет место взаимозависимость реакций. Линейная функция реакции (5.9) хорошо объясняет тенденции взвешенных по рыночной доле конкурирующих цен.
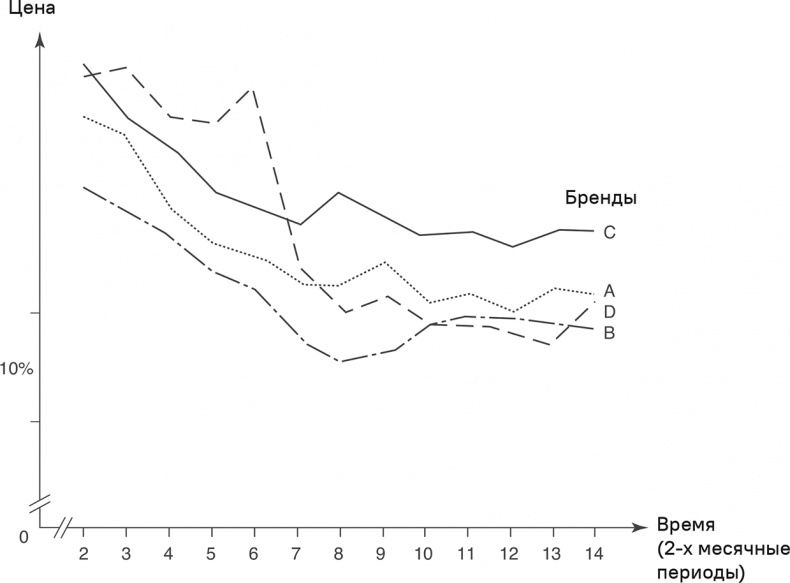
Рис. 5.8. Ценовые тенденции на рынке бытовых чистящих средств
Таблица 5.7. Линейная функция реакции для четырех бытовых чистящих средств
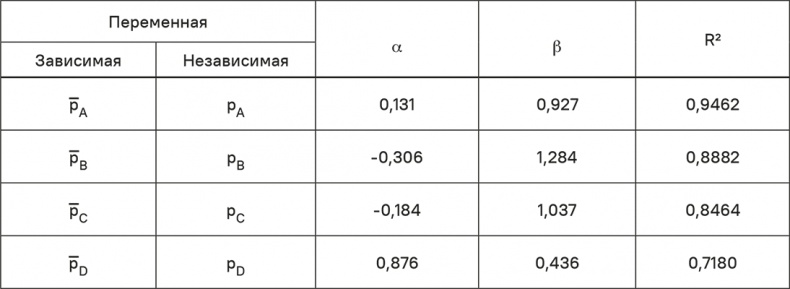
Коэффициенты детерминированности R2 везде высокие, все коэффициенты имеют статистическую значимость на уровне 10 %. Результаты показаны в табл. 5.7.
Чтобы продемонстрировать ценовую детерминированность, мы выбрали бренд D с коэффициентом реакции β = 0,436. Использованная здесь функция «цена-отклик» является вариантом, где разница цен (а не абсолютная цена) служит независимой переменной. Получаем функцию «цена-отклик» для D:
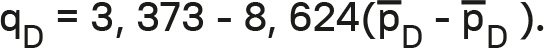
Скорректированная на реакцию максимальная цена для D равна $2,25 за килограмм, то есть скорректированная на реакцию функция «цена-отклик» пересекается с ценовой осью на $2,25. Маржинальные затраты составляют $0,85. Чтобы получить оптимальную цену с учетом конкурентной реакции, берем формулу (5.10) и получаем
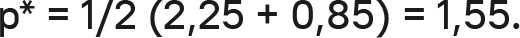
Если конкуренты реагируют согласно прогнозируемой функции, они тоже установят цены (в среднем) на уровне