Рамануджан был брамином, то есть принадлежал к индусской касте, членам которой запрещено наносить вред живым существам. Хотя у его английских друзей сложилось впечатление, что главной его религиозной мотивацией была не вера как таковая, а скорее социальные традиции, он тем не менее соблюдал все надлежащие ритуалы – насколько это было возможно в воюющей Англии. Будучи вегетарианцем, он не доверял университетским поварам и считал, что те недостаточно тщательно исключают из пищи мясные продукты, поэтому научился готовить сам, естественно, в традиционном индийском стиле. По отзывам друзей, он стал великолепным поваром.
Около 1916 г. друг Рамануджана Ганеш Чандра Чаттерджи, стипендиат правительства Индии, собрался жениться, в связи с чем Рамануджан пригласил его с будущей невестой на обед. Как договаривались, Чаттерджи, его невеста и сопровождающая ее женщина появились у него на квартире, и Рамануджан подал гостям суп. Тарелки быстро опустели, и он предложил добавки; все трое согласились. После этого он предложил еще. Чаттерджи согласился, а дамы отказались.
Вскоре после этого Рамануджан куда-то пропал.
Гости ждали его возвращения, но прошел час, а его все не было. Чаттерджи спустился вниз и нашел консьержа. Да, он видел, как мистер Рамануджан подозвал такси и куда-то уехал. Чаттерджи вернулся в комнату, и трое гостей продолжали ждать хозяина до 10 часов вечера, когда, по правилам университета, вынуждены были удалиться. Хозяин так и не появился. Еще четыре дня от него не было ни слуху ни духу… Что произошло? Чаттерджи очень тревожился.
На пятый день пришла телеграмма из Оксфорда: не может ли Чаттерджи выслать Рамануджану телеграфом £5? (В те дни это была немалая сумма, в сегодняшних деньгах соответствует нескольким сотням фунтов.) Деньги были высланы, Чаттерджи ждал, и через надлежащее время Рамануджан появился. На вопрос о том, что же тогда произошло, он объяснил: «Я почувствовал себя обиженным и оскорбленным, оттого что дамы отказались от приготовленной мной пищи».
Это происшествие, очевидно, стало внешним проявлением внутреннего смятения. Рамануджан был на грани срыва. Он так и не смог по-настоящему адаптироваться к жизни в Англии. Его здоровье, которое никогда не отличалось крепостью, ухудшалось, и скоро он оказался в больнице. Харди навестил его там, и этот визит привел к появлению еще одной истории о Рамануджане, в которой тоже фигурирует такси. Это стало для него своего рода клише, но история все же заслуживает внимания.
Харди однажды написал, что каждое положительное целое число было личным другом Рамануджана, и проиллюстрировал это анекдотом о посещении Рамануджана в больнице. «Я приехал к нему в такси номер 1729 и заметил в разговоре, что это число показалось мне каким-то скучным и что, как я надеялся, это не дурная примета. “Нет, – ответил Рамунаджан, – это очень интересное число; это самое маленькое число, которое можно выразить как сумму двух кубов двумя разными способами”».
Если точнее,
1729 = 13 + 123 = 93 + 103,
и это действительно самое маленькое число, обладающее таким свойством.
История колоритная, но я не могу отделаться от ощущения, что со стороны Харди это был подготовленный экспромт; Харди просто пытался подбодрить больного друга, поманив его интересной задачей. Конечно, большинство людей не заметили бы эту особенность числа 1729, но Рамануджан, несомненно, должен был сразу распознать ее. И правда, многие математики, особенно те из них, кто интересуется теорией чисел – и Харди среди них, – должны были знать об этом. Почти невозможно себе представить, чтобы математик, посмотрев на число 1729, не подумал о числе 1728, которое представляет собой 12 в кубе. Трудно также не заметить, что 1000 – это 10 в кубе, а 729 – 9 в кубе.
Как бы то ни было, рассказ Харди привел к появлению в теории чисел не слишком крупной, но интересной концепции: числа такси; n-е число такси есть наименьшее число, которое можно выразить как сумму двух положительных кубов n различными способами. Вот следующие два числа такси:
87 539 319,
6 963 472 309 248.
Чисел такси существует бесконечно много, но известны лишь первые шесть из них.
К 1917 г. Рамануджан вернулся в свои комнаты, одержимый математикой до такой степени, что ничто другое для него уже не имело значения. Он часто работал день и ночь, а затем падал в изнеможении и спал часов 20 подряд. Это не приносило пользы его здоровью, а война вызывала дефицит фруктов и овощей, которыми он питался. К весне Рамануджана поразила какая-то нераспознанная, но, вероятно, неизлечимая болезнь. Его положили в маленькую частную больницу для пациентов из Тринити-колледжа. На протяжении двух следующих лет он консультировался у восьми, если не больше, врачей и побывал по крайней мере в пяти больницах и санаториях. Врачи подозревали язву желудка, затем рак, затем заражение крови; но в конечном итоге решили, что это, скорее всего, туберкулез, и лечили Рамануджана в основном именно от этой болезни.
Рамануджану наконец-то – слишком поздно – досталось академическое признание. Он стал первым индийцем, которого избрали членом Королевского общества, и Тринити-колледж тоже избрал его своим членом. Это придало Рамануджану новые силы, и он вновь взялся за математику. Но здоровье не улучшалось, и были подозрения, что виной тому – климат Англии. В апреле 1919 г. Рамануджан вернулся в Индию. Долгое путешествие не прошло для него даром, и к моменту прибытия в Мадрас здоровье его вновь ухудшилось. В 1920 г. Рамануджан умер в Мадрасе, оставив вдову. Детей у них не было.
* * *
С математикой Рамануджана можно познакомиться по четырем основным источникам: это опубликованные статьи, три переплетенных блокнота, квартальные отчеты Мадрасскому университету и неопубликованные рукописи. Четвертый «утерянный» блокнот – связка разрозненных листков – вновь обнаружил в 1976 г. Джордж Эндрюс, но некоторые рукописи до сих пор не найдены. «Записные книжки Рамануджана» в трех томах, включающие доказательства всех его формул, вышли под редакцией Брюса Берндта.
У Рамануджана была необычная биография и не было формального математического образования. Вряд ли стоит удивляться тому, что его математика весьма специфична. Самой сильной стороной его таланта была немодная область математики – производство остроумных и замысловатых формул. Рамануджан был преимущественно человеком формулы, и в этом ему не было равных, за исключением нескольких старых мастеров, таких как Эйлер или Якоби. «В каждой из формул Рамануджана всегда кроется больше, чем видно на первый взгляд», – писал Харди. Большая часть его результатов имеет отношение к бесконечным рядам, интегралам и цепным дробям. В качестве примера цепной дроби можно привести выражение
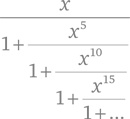
которое было написано на последней странице его письма в составе по-настоящему жуткой, но правильной формулы. Некоторые из своих формул Рамануджан применял в теории чисел, где его особо интересовала аналитическая теория чисел, которая ищет простые приближения для таких величин, как число простых чисел до заданного предела – теорема о простых Гаусса (глава 10) – или среднее число делителей у заданного числа.