Частично объяснение таких больших изменений в производительности представлено на рисунке 8.2. Я переработал эту кривую производительности на рисунке 8.3, отметив разные моменты, которые могут возникнуть во время игры. Представьте себе, что команда находится в положении А. Футболисты прикладывают разумные усилия, но их производительность не увеличивается. Затем Стивен Джеррард или Рой Кин издает боевой клич. Он подталкивает их, заставляет выйти на новый уровень усилий и временно перемещает усилие команды до точки В. В результате производительность поднимается до точки C и команда парит. Но такие усилия неустойчивы. Даже взмахивающие руки Джеррарда или шквал слов из четырех букв от Кина не могут поддерживать такой уровень усилий. Но это не имеет значения – по мере того как уровень усилий снова уменьшается, производительность остается на более высокой линии. Даже когда усилие падает к точке D – до уровня, на котором команда начала, – производительность остается намного лучше прежней.
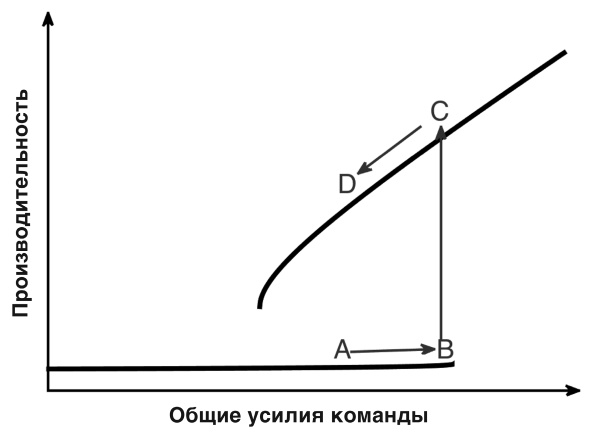
Рисунок 8.3. Кривая производительности команды в футболе. Команда начинает в точке А. По мере того как усилие увеличивается, она перемещается в точку B, после чего производительность переходит к точке C. Усилие теперь может снова уменьшиться, но производительность остается относительно высокой в точке D.
Эти переходы объясняют, почему харизматичный лидер настолько важен для команды. Он или она может поднять общие усилия на небольшой уровень, но этого может быть достаточно для достижения производительности на высшем уровне. Как только уровень производительности будет увеличен, усилия могут немного снизиться, но уровень производительности будет сохранен.
Но мы должны быть осторожны. Переключение в производительности может работать в обратном направлении: самоуспокоенность может просочиться в команду, которая хорошо работает. Представьте, что команда находится в точке D на рисунке 8.3, и их усилия немного уменьшаются. В настоящее время существует риск того, что их производительность снизится на другом конце кривой. Когда он опускается, становится намного сложнее поднять его снова. Команде нужно вернуться к точке А, затем к B, и только потом производительность подскочит снова. Это требует топ-игры от каждого футболиста. Учитывая разные мотивационные факторы у того или иного игрока, достичь этого будет непросто.
Звездное обязательство
Я начал эту главу с вопроса о сотрудничестве. Как футбольные команды, компании и группы животных предотвращают лень? Один вариант ответа был связан с генетическим родством, но идея сверхлинейности Лобановского дает нам альтернативный ответ. Биологи и директора компаний могут действительно учиться у футбольных тренеров. Тренеры не наказывают игроков за то, что те не справляются со своей работой, – вместо этого они создают структуру команды, которая гарантирует выгоду сотрудничества.
Чтобы понять, почему сверхлинейность способствует сотрудничеству, подумайте о проблеме, с которой тренеры сталкиваются постоянно: как заставить игроков участвовать в командном плане. Доходные трансферы и агенты, стремящиеся увеличить зарплаты игроков, обеспечив переход в другое место, – умы футболистов заняты не только мыслью о победе в матче. Классическим примером является недовольная звезда, которая надеется на переход в более состоятельный клуб. Я не буду называть никаких имен, однако мы знаем много футболистов, которые всегда присматриваются к следующему шагу в карьере. Следуя роли, назначенной тренером, такая звезда может сиять не так ярко в индивидуальном плане. Вопрос для нашей звезды заключается в том, лучше ли играть в составе команды или пытаться выглядеть как можно лучше индивидуально. Задача тренера заключается в том, чтобы убедить каждого игрока, что следовать плану команды выгодно.
Рассмотрим команду со сверхлинейной кривой производительности, в которой производительность пропорциональна квадрату усилия, как показано на правом графике на рисунке 8.1. Усилие каждого игрока оценивается по шкале от 0 до 1. Если все игроки вносят 100 %, то сумма их усилий равна 11. Для сверхлинейной кривой производительности эффективность команды составляет 11 × 11 = 121. Если один игрок вносит 0 %, а остальные дают 100 %, тогда сумма становится (10 × 10) + (0 × 1) = 100. Если участвует только один игрок, тогда эффективность равна (1 × 1) + (0 × 10) = 1. Если мы предположим, что игроки трудятся для победы одинаково, то их собственный выигрыш составляет 121/11 = 11. Если все, кроме одного игрока, дают 100 %, результат для каждого равен 100/11 = 9,09. Если же только один прилагает усилия, то показатель будет равен 1/11 = 0,09.
Теперь мы можем рассмотреть, как недовольная звезда рассматривает плюсы и минусы. Дилемма для него заключается не столько в том, будет ли он усердно трудиться на поле, сколько в том, должен ли он прилагать усилия для реализации командного плана. Вместо того чтобы работать в команде, он может пытаться выглядеть хорошо: стараться бить, а не отдавать передачи или избегать оборонительной работы. Предположим, что все усилия, которые он не вложил в команду, могут быть использованы для того, чтобы он выглядел хорошо. В таблице 8.2 приведены выигрыши для звездного игрока, который вкладывает 100 % или 0 % в командные усилия.
Таблица 8.2
Таблица выигрыша для модели «заинтересованности звезды». Ячейки – выигрыши звездного игрока в зависимости от его собственных и командных усилий

Начнем с того, что происходит, когда остальная команда дает 100 %. Если звезда прилагает 100 % усилий, то получает бо́льшую пользу от производительности команды, 11 очков. С другой стороны, если такой игрок не прилагает усилий (0 %), то получает личную славу (+1), при этом команда в целом проигрывает и теперь получает только 9,09 очков. Наша недоработавшая звезда получает в общей сложности 10,09 балла – меньше, чем 11, которые он получил бы, если придерживался плана тренера. Если остальная команда играет по плану, то даже с точки зрения собственного эгоизма звезда должна следовать установке.
У всех игроков, даже у выделывающейся суперзвезды, есть стимул играть на команду, поскольку эффективность команды увеличивается суперлинейно. Когда команда функционирует правильно, но при этом один игрок не играет отведенную ему роль, то страдает вся команда, включая тунеядца. Тот же аргумент имеет место быть, если звезда решает выкладываться на 90 % или любой другой немаксимальный уровень заинтересованности
[86]. Нет смысла играть не на 100 %, если остальные выполняют свою долю работы.
Из этого анализа может показаться, что сотрудничество не должно быть проблемой. Если игроки работают в эффективной команде, а эта эффективность больше, чем сумма эффективности ее частей, то стимул играть свою роль есть у всех. Все, что нужно сделать тренеру, – заставить команду работать вместе, и все будут счастливы. К сожалению для тренера, все немного сложней. Если мы посмотрим на второй столбец в таблице 8.2, мы увидим совсем другую ситуацию. Когда остальная команда не прилагает усилий, что должна делать звезда? Если он выкладывается на 100 %, то его небольшой вклад делится на всех. Звездный игрок выглядит еще хуже, чем в других случаях. Если он дает 0 % в игре на установку, команда все еще терпит неудачу, но он выглядит лучшим из худших. Теперь стимулом является ужасная игра остальных игроков в команде.




