Нильс Бор и комплементарность: из чего состоит природа?
Физик-теоретик Нильс Бор (1885–1962) пришел к выводу, что конечную сущность энергии можно рассматривать по крайней мере с двух сторон. Можно воспринимать ее как частицы (крошечные объекты) или волны (расходящиеся круги). Соответственно, детекторы частиц обнаружат частицы, в то время как волновые детекторы найдут волны. Оба варианта верны, и то, что мы «видим», зависит от инструментов. Мы сами можем решить, какие инструменты использовать и стоит ли мыслить левым полушарием, сосредоточенным на составных элементах, или правым, которое видит динамическое целое и тенденции. На рис. 2.7 слева показан преобладающий, левополушарный, вертикальный и ориентированный на частицы подход, а дополнительный, правополушарный, латеральный и ориентированный на волны подход — справа. Музыку можно считать нотной партитурой (слева) или грохочущими звуковыми волнами, которые производит оркестр (справа). Между полушариями существует парадоксальное различие. Представляется, что правое полушарие знает о существовании первого, но левое нередко игнорирует правое. Пациенты с поврежденным правым полушарием часто настаивают, что с ними все в порядке. Пациенты с поврежденным левым полушарием горюют об утраченных способностях. В этой книге мы стараемся с помощью волн спасти нас от ограничений, наложенных частицами и аналитическим мышлением. Чтобы понять инновации, стоит представлять их как интерференцию пересекающихся волн, образующих приятные глазу узоры.
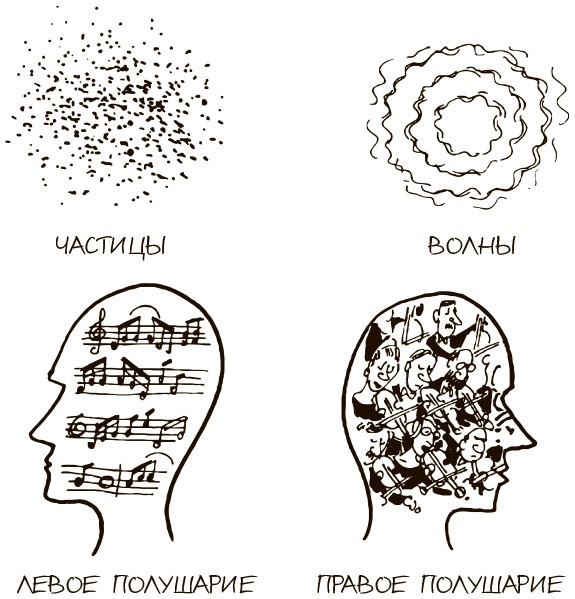
Рис. 2.7. Комплементарное устройство природы
Как же нам быть в мире, который порой имеет волновую, а порой корпускулярную природу — в зависимости от наших инструментов? Здесь важно понять, что нет единственной, «богом данной» реальности. Наши глаза — не зеркала, отражающие эту «реальность». Вся наука и все знания — это взаимодействие между человеческой нервной системой и природными явлениями (см. рис. 2.8).
Рис. 2.8. Взаимодействие между человеческой нервной системой и природными явлениями
Например, цвет — это атрибут не предметов, а нас самих. Мы машем красной мулетой перед быками, но они не различают цветов. Их раздражает сам факт того, что перед ними чем-то машут. Более того, зрение отчасти подчиняется нашим намерениям. Например, когда женщина беременна, она видит больше вещей, связанных с детьми, чем замечала до того. Словом, мы до некоторой степени выбираем, видеть ли волны или частицы, — и используем соответствующие инструменты. Не бывает внимания без намерения. Новаторы видят вещи по-новому, потому что им так хочется и потому что «непроторенная дорога» почти всегда интереснее.
Случайность и эволюция: множество Мандельброта
Одно из самых поразительных и загадочных проявлений Вселенной — необыкновенная симметрия, красота и гармония природного мира. Однако мы все меньше и меньше верим в божественное происхождение объектов в природе. Но если его нет, как же они появились? Откуда взялись колибри, павлин, паутина паука-крестовика, которая в относительном выражении в десять раз прочнее стали и гораздо гибче ее? В самом деле, творения природы с огромным избытком превосходят все созданное людьми-новаторами. Так в чем секрет их появления и может ли бизнес использовать их как пример и объект для подражания? Давайте попытаемся рассмотреть паттерны эволюционного процесса. Французский математик Бенуа Мандельброт (1924–2010), известный благодаря «теории шероховатости» и множествам Мандельброта, попытался симулировать эволюцию с помощью компьютерной программы и получил потрясающие результаты.
Для начала нам необходимо понять фрактальную природу Вселенной. Что такое фрактал? Очевидным примером может послужить дерево. У него есть ствол, сучья, ветки и листья, и оно уникально, поскольку двух одинаковых деревьев не бывает. Его очертания закодированы в каждом листе — прожилки напоминают ветки. Корни похожи на само дерево, только перевернутое. Дерево самоподобное, но другое; закономерное, но исключительное; упорядоченное, но хаотичное; симметричное, но не вполне. Казалось бы, это невозможно — как у природы получается повторять себя и одновременно вносить изменения? Однако это может произойти — и происходит. Более того, книга, которую вы сейчас читаете, тоже фрактальна. Организующий ее цикл постоянно повторяется и меняется.
На рис. 2.9 мы видим фракталы, которые встречаются в природе.

Рис. 2.9. Шесть фрактальных форм и узоров
• Возьмите снежинку (слева вверху). Она уникальна — невозможно найти две полностью одинаковые. Пока кристаллы-затравки падают с неба, они собирают замерзающие частички, пристающие к самым коротким и теплым лучам, и поэтому лучи симметричны, но лишь приблизительно. Снежинка проходит сквозь слои то более холодного, то более теплого воздуха разной влажности, поэтому к ее лучам приклеивается то больше, то меньше частичек — опять-таки в зависимости от состояния воздуха и более-менее симметрично. Но фактор случайности присутствует постоянно. Смена воздушных слоев может быть внезапной, и тогда снежинка опустится на землю, не сформировавшись. В порядке здесь присутствует произвольность, а в случайности — закономерность.
• Справа вверху показаны записанные электроэнцефалографом мозговые волны женщины, решающей математическую задачу в семь действий. Когда она расслаблена, ее мозговые волны тоже фрактальны, но проще и гораздо спокойнее.
• Слева в середине изображены дендриты в человеческом мозге — они похожи на маленькие перевернутые деревья.
• Справа в середине показан пульс здорового человеческого сердца, который постоянно меняется в зависимости от возникающих задач — он одновременно хаотичный и постоянный.
• Слева внизу изображена система кровообращения, которая прогоняет кровь по нашему телу через десятки тысяч крошечных капилляров, и благодаря этому мы краснеем, если смущены или если нас шлепнут.
• Справа внизу — широко известная «Большая волна» с гравюры японского художника Хокусая. Ее форма повторяется в пене гребней. В правом нижнем углу изображен нос лодки, на которой людей (невидимых на этом фрагменте) по воле волн подбрасывает вверх и вниз во фрактальной Вселенной.
Если наши мозги, тела и искусство фрактальны, может быть, бизнес тоже должен быть фрактальным? И как сымитировать разворачивающийся эволюционный узор фракталов на компьютере? Мандельброт вывел математическое уравнение, которое задает последовательность постоянно меняющихся результатов (рис. 2.10).
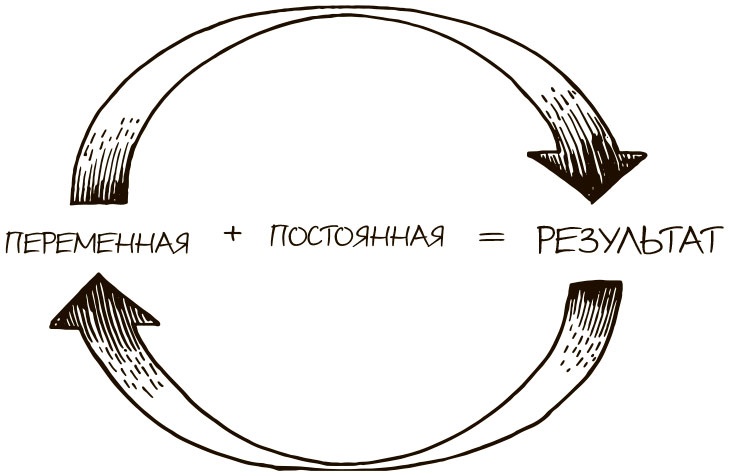
Рис. 2.10. Математическая формула в центре инноваций






