Ночью я открываю мой люк и смотрю, как далеко
разбрызганы
в небе миры,
И все, что я вижу, умноженное на сколько хотите, есть
только
граница новых и новых вселенных.
Дальше и дальше уходят они, расширяясь, всегда
расширяясь,
За грани, за грани, вечно за грани миров.
Как далеко ни смотри, за твоею далью есть дали.
Считай, сколько хочешь, неисчислимы года.
(Уолт Уитмен)
Представление о бесконечности окружающего мира кажется очень естественным. Ведь, действительно,
…коль признать, что пространство вселенной конечно,
То если б кто-нибудь вдруг, разбежавшись в стремительном
беге,
Крайних пределов достиг и оттуда, напрягши все силы,
Бросил с размаху копье, то, — как ты считаешь? — оно бы
Вдаль полетело, стремясь неуклонно к намеченной цели,
Или же что-нибудь там на пути ему помешало?
(Тит Лукреций Кар)
В I веке до н. э. Лукреций сформулировал и другой аргумент в пользу бесконечности Вселенной:
…если все необъятной вселенной пространство
Замкнуто было б кругом и, имея предельные грани,
Было б конечным, давно уж материя вся под давленьем
Плотных начал основных отовсюду осела бы в кучу,
И не могло бы ничто под покровом небес созидаться;
Не было б самых небес, да и солнца лучи не светили б,
Так как материя вся, оседая все ниже и ниже
От бесконечных времен, лежала бы сбившейся в кучу.
Заменяем у Лукреция слово «давление» на «гравитация» и получаем описание гравитационной неустойчивости. Вот, к примеру, как об этом же писал Ньютон: «Мне представляется, что если бы вещество нашего Солнца и планет, да и все вещество Вселенной было бы равномерно рассеяно по всему небу, и каждая частица обладала бы внутренне присущим ей тяготением ко всем остальным, а все пространство, по которому было бы рассеяно это вещество, было бы конечным, то вне этого пространства вещество под действием своего тяготения стремилось бы ко всему веществу внутри него и, следовательно, падало бы к центру пространства и образовало бы там одну гигантскую сферическую массу».
Итак, пусть бесконечная стационарная Вселенная равномерно заполнена звездами, причем n — среднее число звезд в единице объема, a L — средняя светимость одной звезды, то есть полная энергия, излучаемая ею в единицу времени во всех направлениях. Рассмотрим звезду на расстоянии r от Земли. Освещенность, то есть поток энергии, приходящийся на единицу площади, от этой звезды на поверхности Земли равна
E (r) = L /4π r2 (1)
Смысл этой формулы очень прост — излучаемая звездой энергия распределяется по поверхности сферы радиуса r, площадь которой равна 4πr2 .
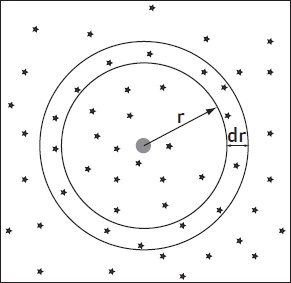
Рис. 1. Сферический слой, вырезанный в бесконечной Вселенной
Теперь рассмотрим окружающий Землю концентрический слой радиусом r и толщиной dr — см. рис. 1. Объем этого слоя равен 4πr2dr (это просто произведение площади сферы радиуса r на толщину слоя) и, следовательно, в нем находятся n · 4πr2dr звезд. В итоге получаем, что полная освещенность от звезд этого слоя
dE (r) = n · 4πr2dr · L/ 4πr2 = nLdr (2)
Любопытный факт — мы обнаружили, что суммарная освещенность от звезд, расположенных в каком-либо сферическом слое, зависит только от толщины этого слоя (dr), и не зависит от расстояния до него. Причиной является то, что, по мере удаления слоя, уменьшение освещенности от составляющих его звезд в точности компенсируется ростом числа звезд в слое (формула (2)).
Таким образом, если мы разбили Вселенную на слои одинаковой толщины, то каждый такой слой дает одинаковый вклад в освещенность на Земле. Вселенная бесконечна, а, значит, и число таких слоев бесконечно. Отсюда простой вывод — освещенность, создаваемая всеми объектами бесконечной Вселенной, бесконечна. Результат обескураживающий. Бесконечная яркость ночного неба очевидным образом противоречит повседневному опыту. Парадокс?
Попробуем сделать нашу модельную Вселенную более реалистичной. Учтем, что звезды не являются математическими точками, а имеют хотя и очень малый, но конечный угловой размер. Например, угловой размер нашего Солнца с расстояния 1 парсек (примерно 3.3 светового года) равен 0,01'' (одна сотая угловой секунды) — величина, безусловно, очень маленькая, но не нулевая. Это означает, что ближайшие к нам звезды загораживают более далекие и экранируют их излучение. Для иллюстрации этого утверждения обычно используют сравнение заполненного звездами пространства с густым лесом. Находясь в глубине леса, вы со всех сторон окружены деревьями. Если лес небольшой, то между стволами деревьев будут видны просветы. Если же лес очень большой и густой, то стволы ближайших деревьев сплошной стеной прикроют от вас все, что находится вдали.
Следовательно, в бесконечной Вселенной любой луч зрения рано или поздно упрется в диск какой-нибудь звезды и поэтому ночное небо должно равномерно сверкать как диск типичной звезды. Это уже лучше, чем бесконечная яркость, однако совсем не похоже на реальное ночное небо. Действительно, предположим, что Солнце — обычная средняя звезда (это и в самом деле близко к действительности). Тогда небосвод, точнее, полусфера, доступная наблюдениям, должен сиять примерно в 100 000 раз ярче, чем Солнце. Столь мощное излучение сделало бы невозможным не только обсуждение яркости ночного неба, но и вообще исключило бы появление жизни на нашей планете.
Описанный парадокс был осознан уже несколько столетий назад. Он носит название фотометрического парадокса или парадокса Ольберса. Как будет ясно из дальнейшего, Ольберс был далеко не первым исследователем, обратившим внимание на эту загадку, но, к сожалению, очень часто законы, формулы и вообще любые открытия носят имена не своих первооткрывателей — вспомним, к примеру, открытие Америки. Английский физик Майкл Берри в шутку сформулировал принцип Арнольда (в честь знаменитого российского математика В. И. Арнольда): если какой-нибудь предмет или понятие имеет персональное имя, то это — не имя первооткрывателя.
В свою очередь, принцип Берри гласит, что принцип Арнольда применим и к самому себе
[3].



