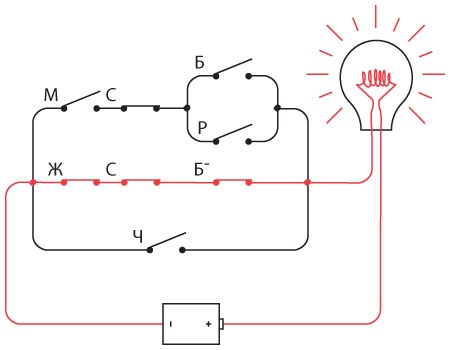
Так можно замкнуть все нужные переключатели, зажечь лампочку и показать, что котенок удовлетворяет всем вашим критериям.
Джордж Буль никогда не собирал такую схему. Ему никогда не доводилось видеть логическое выражение, реализованное с помощью переключателей, проводов и лампочек. Разумеется, одним из препятствий было то, что лампа накаливания была изобретена только спустя 15 лет после смерти Буля. Однако Сэмюэл Морзе продемонстрировал свой телеграф в 1844 году — за десять лет до публикации книги Буля «Исследование законов мышления», и ему ничего не стоило заменить лампочки в приведенной выше схеме клопфером.
Никому в XIX веке не удалось уловить связь между булевыми операциями И и ИЛИ и последовательным и параллельным соединением простых переключателей — ни математику, ни электрику, ни оператору телеграфа
[16]. Это не пришло в голову даже отцу-основателю компьютерной революции — Чарльзу Бэббиджу (1792–1871), который переписывался с Булем и был знаком с его работой, а большую часть жизни потратил на разработку разностной, а затем аналитической машины, которая спустя столетие будет считаться предшественником современных компьютеров. Сейчас мы знаем, что Бэббиджу помогло осознание того, что вместо шестеренок и рычагов для выполнения вычислений лучше использовать телеграфные реле.
Да, телеграфные реле.
Глава 11
Логические вентили
В далеком будущем, когда история примитивных вычислений XX века превратится в предания, кто-то, вероятно, предположит, что логические вентили были названы в честь одноименного сантехнического устройства. Это не совсем так. Мы вскоре увидим, что логические вентили действительно напоминают обычные вентили, через которые проходит вода, и выполняют элементарные логические задачи, блокируя или пропуская электрический ток.
В предыдущей главе мы рассматривали сценарий, когда вы вошли в зоомагазин и сказали продавцу: «Мне нужен белый или рыжий стерилизованный кот или стерилизованная кошка любого цвета, кроме белого, или любой кот или кошка черного цвета». Эти критерии можно объединить в следующее логическое выражение, а также выразить с помощью схемы из переключателей и лампочки:
(М × С × (Б + Р)) + (Ж × С × (1 − Б)) + Ч.
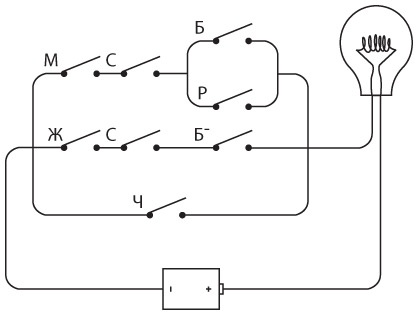
Такая схема иногда называется сетью, хотя в настоящее время это слово гораздо чаще используется для обозначения соединенных между собой компьютеров, а не набора простых переключателей.
Несмотря на то что все обозначенные на схеме элементы были изобретены в XIX веке, тогда никто не представлял, что логические выражения можно реализовать непосредственно в виде электрических цепей. Эта возможность была осознана только в 1930-х годах Клодом Шенноном (1916–2001), который в 1938 году защитил знаменитую магистерскую диссертацию под названием «Символьный анализ реле и коммутаторов». Спустя десять лет впервые была опубликована его статья «Математическая теория связи», в которой слово «бит» (bit) использовалось для обозначения двоичной цифры.
Разумеется, задолго до 1938 года было известно, что для протекания тока при последовательном соединении двух переключателей оба должны быть замкнуты, а при параллельном соединении — лишь один из них. Однако никто так ясно и убедительно, как Шеннон, не показал, что для проектирования схем с переключателями инженеры-электрики могут использовать все инструменты булевой алгебры. В частности, если вы можете упростить логическое выражение, описывающее схему, то можете упростить и саму схему.
Например, выражение, содержащее ваши критерии выбора кошки, выглядит так:
(М × С × (Б + Р)) + (Ж × С × (1 − Б)) + Ч.
Используя сочетательный закон, мы можем изменить порядок переменных, объединенных знаком И («×»), и переписать выражение:
(С × М × (Б + Р)) + (С × Ж × (1 − Б)) + Ч.
Для ясности введу два дополнительных символа X и Y:
X = М × (Б + Р);
Y = Ж × (1 − Б).
Теперь выражение с критериями выбора кошки можно записать так:
(С × X) + (С × Y) + Ч.
Наконец, мы можем вернуть значения выражений, соответствующих символам X и Y.
Обратите внимание: переменная С встречается в выражении дважды. Используя распределительный закон, это выражение можно переписать только с одной переменной С:
(С × (X + Y)) + Ч.
Теперь подставим в выражение значения X и Y:
(С × ((M × (Б + Р)) + (Ж × (1 − Б)))) + Ч.
Из-за множества скобок это выражение не выглядит упрощенным. Однако оно содержит на одну переменную меньше, а значит, в схеме меньше переключателей. Вот ее пересмотренная версия.
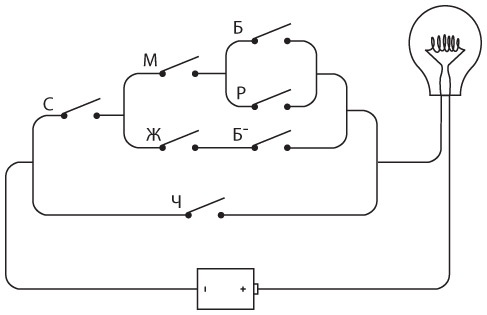
Действительно, увидеть, что эта схема эквивалентна предыдущей, легче, чем заметить тождество выражений.
На самом деле в этой цепи по-прежнему на три переключателя больше, чем нужно. Теоретически для выбора идеальной кошки должно быть достаточно четырех переключателей. Почему четырех? Каждый переключатель — это бит. Одного переключателя хватит для указания пола (разомкнутый — соответствует коту, замкнутый — кошке), еще один будет указывать на стерилизованную кошку в замкнутом состоянии и нестерилизованную — в разомкнутом, еще два позволят распознать цвет. Существуют четыре возможных цвета: белый, черный, рыжий и «другой». И мы знаем, что четыре варианта можно определить с помощью двух битов, поэтому для указания цвета нужно всего два переключателя. Например, белому цвету могут соответствовать два разомкнутых переключателя, черному — один замкнутый, рыжему — второй замкнутый, а «другим» — два замкнутых.
Теперь давайте построим пульт управления для выбора кошки, который будет состоять из лампочки и четырех переключателей (похожих на те, с помощью которых вы включаете и выключаете свет).
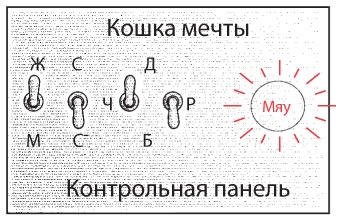
Переключатель замкнут, когда находится в положении вверх, разомкнут — когда находится в положении вниз. Боюсь, что обозначения двух переключателей для выбора цвета кошки могут показаться немного непонятными, однако это следствие попытки обойтись при создании пульта управления минимумом средств. Левый переключатель в этой паре обозначен буквой Ч; замыкание только левого переключателя (как показано на рисунке) соответствует черному цвету. Правый переключатель в этой паре обозначен буквой Р; замыкание только правого переключателя соответствует рыжему цвету, замыкание обоих — «другому» цвету (этот вариант обозначен буквой Д). Размыкание обоих переключателей соответствует белому цвету и обозначается буквой Б внизу.






